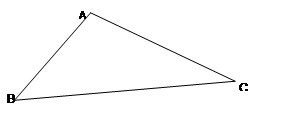
本区某校对学生开展“不闯红灯,珍爱生命”的教育,为此校学生会委员在某天到市中心某十字路口,观察、统计上午7∶00~12∶00之间闯红灯的人次,制作了如下两个统计图:
(1)图一中各时段闯红灯人次的平均数为 人次,中位数是 人次;
(2)该路口这一天上午7∶00~12∶00闯红灯的未成年人有 人次;
(3)估计一周(七天)内该路口上午7∶00~12∶00闯红灯的中青年约有 人次;
(4)是否能以此估计全市这一天上午7∶00~12∶00所有路口闯红灯的人次?为什么?
若干学生分住宿舍,每间4人余20人;每间住8人有一间不空也不满,则宿舍有多少间?学生多少人?
如图,在矩形 中,点
中,点 分别在边
分别在边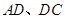 上,
上,
 ,求
,求 的长
的长
小明学了勾股定理后很高兴,兴冲冲的回家告诉了爸爸:在△ABC 中,若∠C=90°, BC =" a" , AC =" b" , AB=c,如下图,根据勾股定理,则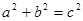 。爸爸笑眯眯地听完后说:很好,你又掌握了一样知识,现在考考你,若不是直角三角形,那勾股定理还成不成立?若成立,请说明理由;若不成立,请你类比勾股定理,试猜想
。爸爸笑眯眯地听完后说:很好,你又掌握了一样知识,现在考考你,若不是直角三角形,那勾股定理还成不成立?若成立,请说明理由;若不成立,请你类比勾股定理,试猜想 与
与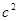 的关系,并选择其中一种情况给予证明。〔下图备用)
的关系,并选择其中一种情况给予证明。〔下图备用)
大众服装店今年4月用4000元购进了一款衬衣若干件,上市后很快售完,服装店于5月初又购进同样数量的该款衬衣,由于第二批衬衣进货时价格比第一批衬衣进货时价格提高了20元,结果第二批衬衣进货用了5000元第一批衬衣进货时的价格是多少?
第一批衬衣售价为120元/件,为保证第二批衬衣的利润率不低于第一批衬衣的利润率,那么第二批衬衣每件售价至少是多少元?
(提示:利润=售价﹣成本,利润率= )
)
如图,△ABC中,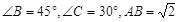 ;求AC的长.
;求AC的长.