如图,P为正方形ABCD的对称中心,A(0,3),B(1,0),直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以 个单位每秒速度运动,运动时间为t.
个单位每秒速度运动,运动时间为t.
求:(1)C点的坐标为 ;
(2)当t为何值时,△ANO与△DMR相似?
(3)①求△HCR面积S与t的函数关系式;
②并求以A、B、C、R为顶点的四边形是梯形时t的值及S的值.
(本大题满分8分,每小题4分)
(1)计算:  (2)解方程:
(2)解方程:
(本题10分)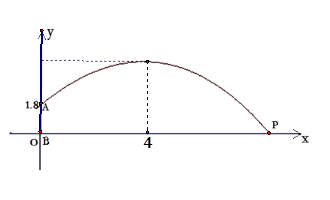 在校际运动会上,身高1.8米的李梦晨(AB)同学,把铅球抛到离脚底(B)9米远的P点,李梦晨同学所抛的铅球在到达最大高度时,距其脚底(B)4米,聪明的你,请你参照图示,帮助李梦晨同学求出此铅球运动的轨迹方程.
在校际运动会上,身高1.8米的李梦晨(AB)同学,把铅球抛到离脚底(B)9米远的P点,李梦晨同学所抛的铅球在到达最大高度时,距其脚底(B)4米,聪明的你,请你参照图示,帮助李梦晨同学求出此铅球运动的轨迹方程.
.(本题8分)
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且
∠DBA=∠BCD.
(1)根据你的判断:BD是⊙O的切线吗?为什么?.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,
且△BEF的面积为10,cos∠BFA= ,那么,你能求
,那么,你能求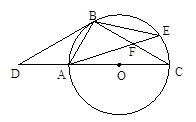 出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
(本题10分)
据我们调查,连云港市“欣欣”家电商场电视柜,今年一月至六月份销售型号为“HH-2188X”的长虹牌电视机的销量如下:
| 月 份 |
一 |
二 |
三 |
四 |
五 |
六 |
| 销量(台) |
50 |
51 |
48 |
50 |
52 |
49 |
一、求上半年销售型号为“HH-2188X”的长虹牌电视机销售量的平均数、中位数、众数;
二、由于此型号的长虹牌电视机的质量好,消费者满意度很高,商场计划八月份销售此型号的电视机72台,与上半年平均月销售量相比,七、八月销售此型号的电视机平均每月的增长率是多少?
.(本题15分)
马田同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),通过计算∠APB的度数,她惊奇的发现∠APB的度数的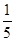 ,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你:
,正好都和她今天作业中的一条抛物线与x轴的交点的横坐标完全相同,她作业中的那条抛物线还经过点C(10,17).聪明的你: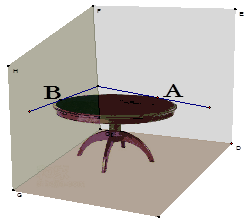 (1)请你求出∠APB的度数
(1)请你求出∠APB的度数
(2)请你求出马田同学作业中的
那条抛物线的对称轴方程.