如图所示,在 坐标系坐标原点O处有一点状的放射源,它向
坐标系坐标原点O处有一点状的放射源,它向 平面内的
平面内的 轴上方各个方向发射
轴上方各个方向发射 粒子,
粒子, 粒子的速度大小均为
粒子的速度大小均为 ,在
,在 的区域内分布有指向
的区域内分布有指向 轴正方向的匀强电场,场强大小为
轴正方向的匀强电场,场强大小为 ,其中
,其中 与
与 分别为
分别为 粒子的电量和质量;在
粒子的电量和质量;在 的区域内分布有垂直于
的区域内分布有垂直于 平面向里的匀强磁场,
平面向里的匀强磁场,
 为电场和磁场的边界.
为电场和磁场的边界. 为一块很大的平面感光板垂直于
为一块很大的平面感光板垂直于 平面且平行于
平面且平行于 轴,放置于
轴,放置于 处,如图所示.观察发现此时恰好无粒子打到
处,如图所示.观察发现此时恰好无粒子打到 板上.(不考虑
板上.(不考虑 粒子的重力及粒子间的相互作用),求:
粒子的重力及粒子间的相互作用),求:
(1) 粒子通过电场和磁场边界
粒子通过电场和磁场边界
 时的速度大小及距y轴的最大距离;
时的速度大小及距y轴的最大距离;
(2)磁感应强度 的大小;
的大小;
(3)将 板至少向下平移多大距离才能使所有的粒子均能打到板上?此时ab板上被
板至少向下平移多大距离才能使所有的粒子均能打到板上?此时ab板上被 粒子打中的区域的长度.
粒子打中的区域的长度.
如图所示,MN表示真空室中垂直于纸面放置的感光板,它的一侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度大小为B. 一个电荷量为q的带电粒子从感光板上的狭缝O处以垂直于感光板的初速度v射入磁场区域,最后到达感光板上的P点. 经测量P、O间的距离为l,不计带电粒子受到的重力。求:
①带电粒子所受洛伦兹力的大小;
②此粒子的质量大小。
(12分)把一小球从离地面 处,以
处,以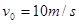 的初速度水平抛出,不计空气阻力, (g=10m/s2)。求:
的初速度水平抛出,不计空气阻力, (g=10m/s2)。求:
(1)小球在空中飞行的时间;
(2)小球落地点离抛出点的水平距离;
(3)小球落地时的速度大小。
(12分)如图所示,质量为80kg的滑雪运动员,在倾角 为30°的斜坡顶端,从静止开始匀加速下滑50m到达坡底,用时10s.若g取10m/s2,求:
为30°的斜坡顶端,从静止开始匀加速下滑50m到达坡底,用时10s.若g取10m/s2,求:
(1)运动员下滑过程中的加速度大小;
(2)运动员到达坡底时的速度大小;
(3)运动员受到的阻力大小。
如图8所示,质量为m=0.2kg的小物体放在光滑的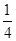 圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角
圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角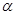 =37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:
=37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:
(1)物体第一次滑到水平轨道与右侧斜面轨道交接处的速度大小
(2)物体第一次滑上右侧斜轨道的最大高度(取g=10m/s2,cos37°=0.8,sin37°=0.6)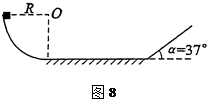
2007年10月24日,“嫦娥一号”探月卫星发射成功,实现了中华民族千年的奔月梦想.2007年11月5日,“嫦娥一号”探月卫星变轨成功,开始绕月球做匀速圆周运动.已知探月卫星距月球表面的高度为h,绕月球做匀速圆周运动的周期为T,月球的半径为R,引力常量为G,忽略其他天体对探月卫星的引力作用.试求:
(1)探月卫星线速度的大小
(2)月球第一宇宙速度的大小