如图，抛物线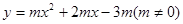
的顶点为H，与
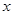轴交于A、B两点（B点在A点右侧），点H、B关于直线：
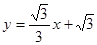对称，过点B作直线BK∥AH交直线于K点．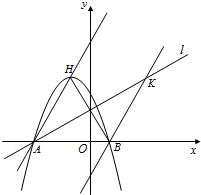 
（1）求A、B两点坐标，并证明点A在直线上；
（2）求此抛物线的解析式；
（3）将此抛物线向上平移，当抛物线经过K点时，设顶点为N，求出NK的长．
关于x的方程x2－2（k－1）x＋k2 = 0的两实根x1、x2满足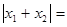
x1x2－1.点A为直线y =" x" 上一点，过A作AC⊥x轴交x轴于C，交双曲线
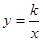于B，求OB2－AB2的值。
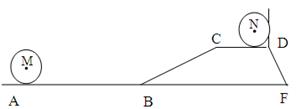
有一河堤坝BCDF为梯形，斜坡BC坡度iBC =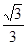 
，坝高为5 m，坝顶CD =" 6" m，现有一工程车需从距B点50 m的A处前方取土，然后经过B—C—D放土,为了安全起见，工程车轮只能停在离A、D处1 m的地方即M、N处工作，已知车轮半经为1 m，求车轮从取土处到放土处圆心从M到N所经过的路径长。（tan150=2－
）
|
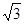为实施“农村留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名，2名，3名，4名，5名，6名共六种情况，并制成如下两幅不完整的统计图。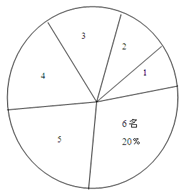
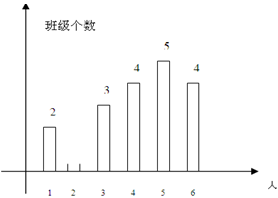
全校留守儿童班级数扇形统计图全校留守儿童人数条形统计图
（1）.求该校平均每班有多少留守儿童？并将条形补全。
（2）.某爱心人士，决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名儿童来自同一班级的概率。
已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E。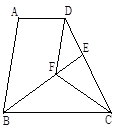
求证：（1）△BFC≌△DFC；（2）AD=DE
阅读以下材料：
对于三个数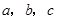
，用
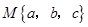表示这三个数的平均数，用
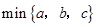表示这三个数中最小的数．例如：
；
；
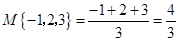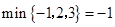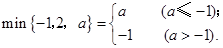
解决下列问题：
（1）填空：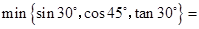
；
（2）①如果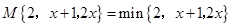
，求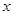
；
②根据①，你发现了结论：
“如果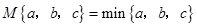
，那么（填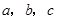的大小关系）”．
③运用②的结论，填空：
若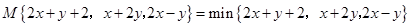
，则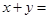
．
（3）填空：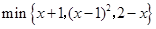
的最大值为．