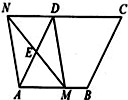
如图,在菱形 中,
中,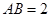 ,
, ,点
,点 是
是 边的中点,点
边的中点,点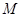 是
是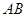 边上一动点(不与点
边上一动点(不与点 重合),延长
重合),延长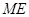 交射线
交射线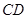 于点
于点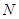 ,连接
,连接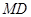 ,
,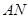 .
.
(1)求证:四边形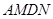 是平行四边形;
是平行四边形;
(2)填空:①当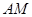 的值为 时,四边形
的值为 时,四边形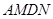 是矩形;
是矩形;
②当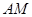 的值为 时,四边形
的值为 时,四边形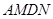 是菱形.
是菱形.
今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A、
B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;
从B地到甲地60千米,到乙地45千米.
⑴设从A水库调往甲地的水量为x万吨,完成下表

|
甲 |
乙 |
总计 |
||||||
| A |
x |
14 |
|||||||
| B |
14 |
||||||||
| 总计 |
15 |
13 |
28 |
⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)
有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记
下花色和数字后将牌放回,洗匀后乙再抽取一张.
⑴先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率.
⑵甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.
请问甲选择哪种方案胜率更高?
如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D
点作DE⊥DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.
为了加强食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用油共抽
18瓶进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以
下折线统计图和扇形统计图.
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶乙品牌食用油,请估计能买到“优秀”等级的概率是多少?
如图l0.在平面直角坐标系xoy中,AB在x轴上,AB=10.以AB为直径的⊙O’与y轴正半轴交于点C.连接BC,AC。CD是⊙O’的切线.AD⊥CD于点D,tan∠CAD=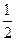 ,抛物线
,抛物线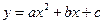 过A、B、C三点。
过A、B、C三点。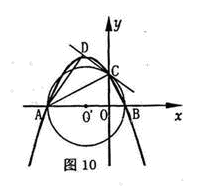
(1)求证:∠CAD=∠CAB;
(2)①求抛物线的解析式;
②判断抛物线的顶点E是否在直线CD上.并说明理由:
(3)在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在.请说明理由.