如图,在四棱锥P-ABCD中,底面ABCD是正方形,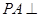 底面
底面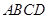 ,且PA=AB.
,且PA=AB.

(1)求证:BD 平面PAC;
平面PAC;
(2)求异面直线BC与PD所成的角.
(本小题满分12分)
已知数列 ,
, 满足:
满足: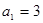 ,当
,当 时,
时,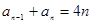 ;对于任意的正整数
;对于任意的正整数 ,
,
 .设数列
.设数列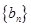 的前
的前 项和为
项和为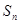 .
.
(Ⅰ)计算 、
、 ,并求数列
,并求数列 的通项公式;
的通项公式;
(Ⅱ)求满足 的正整数
的正整数 的集合.
的集合.
(本小题满分12分)
在平面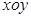 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为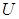 ,不等式组
,不等式组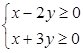 确定的平面区域为
确定的平面区域为 .
.
(Ⅰ)定义横、纵坐标为整数的点为“整点”. 在区域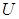 任取3个整点,求这些整点中恰有2个整点在区域
任取3个整点,求这些整点中恰有2个整点在区域 的概率;
的概率;
(Ⅱ)在区域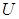 每次任取
每次任取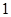 个点,连续取
个点,连续取 次,得到
次,得到 个点,记这
个点,记这 个点在区域
个点在区域 的个数为
的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
.(本小题满分12分)
已知函数 .
.
(Ⅰ)求函数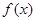 的最大值,并写出
的最大值,并写出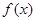 取最大值时
取最大值时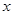 的取值集合;
的取值集合;
(Ⅱ)已知 中,角
中,角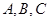 的对边分别为
的对边分别为 若
若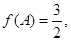
 求实数
求实数 的最小值.
的最小值.
(本小题满分10分)选修4—5:不等式选讲
设函数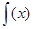 =
=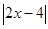 + 1.
+ 1.
(Ⅰ)画出函数y=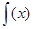 的图像:
的图像:
(Ⅱ)若不等式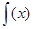 ≤ax的解集非空,求n的取值范围
≤ax的解集非空,求n的取值范围
(本小题满分10分)选修4—4;坐标系与参数方程.
在平面直角坐标系 中,曲线
中,曲线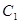 的参数方程为
的参数方程为 (
( ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线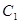 上的点
上的点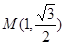 对应的参数
对应的参数 ,射线
,射线 与曲线
与曲线 交于点
交于点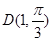 .
.
(I)求曲线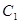 ,
, 的方程;
的方程;
(II)若点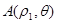 ,
, 在曲线
在曲线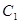 上,求
上,求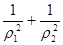 的值.
的值.