一个盒子中装有4个编号依次为1、2、3、4的球,这4个球除号码外完全相同,先从盒子中随机取一个球,该球的编号为X,将球放回袋中,然后再从袋中随机取一个球,该球的编号为Y
(1)列出所有可能结果。
(2)求事件A=“取出球的号码之和小于4”的概率。
(3)求事件B=“编号X<Y”的概率
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API |
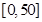 |
 |
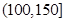 |
 |
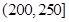 |
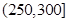 |
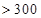 |
| 空气质量 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中重度污染 |
重度污染 |
| 天数 |
4 |
13 |
18 |
30 |
9 |
11 |
15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为w)的关系式为: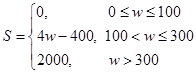 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染完成下面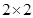 列联表,并判断能否有
列联表,并判断能否有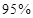 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
附:
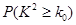 |
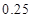 |
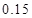 |
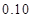 |
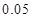 |
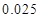 |
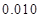 |
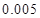 |
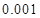 |
 |
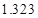 |
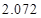 |
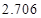 |
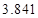 |
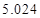 |
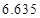 |
 |
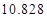 |
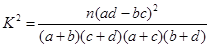
| 非重度污染 |
重度污染 |
合计 |
|
| 供暖季 |
|||
| 非供暖季 |
|||
| 合计 |
100 |
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA 底面ABCD,且SA=2,AD=DC=1
底面ABCD,且SA=2,AD=DC=1
(1)若点E在SD上,且 证明:
证明: 平面
平面 ;
;
(2)若三棱锥S-ABC的体积 ,求面SAD与面SBC所成二面角的正弦值的大小
,求面SAD与面SBC所成二面角的正弦值的大小
三角形ABC中,内角A、B、C所对的边a、b、c成公比小于1的等比数列,且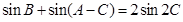 .(1)求内角B的余弦值;(2)若
.(1)求内角B的余弦值;(2)若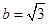 ,求三角形
,求三角形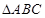 的面积.
的面积.
已知函数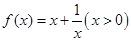 ,以点
,以点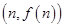 为切点作函数图像的切线
为切点作函数图像的切线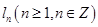 ,直线
,直线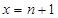 与函数
与函数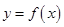 图像及切线
图像及切线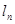 分别相交于
分别相交于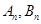 ,记
,记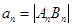 .
.
(1)求切线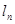 的方程及数列
的方程及数列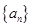 的通项;
的通项;
(2)设数列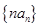 的前
的前 项和为
项和为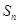 ,求证:
,求证: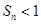 .
.
已知 的三个顶点都在抛物线
的三个顶点都在抛物线 上,且抛物线的焦点
上,且抛物线的焦点 满足
满足 ,若
,若 边上的中线所在直线
边上的中线所在直线 的方程为
的方程为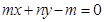 (
( 为常数且
为常数且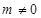 ).
).
(1)求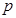 的值;
的值;
(2)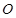 为抛物线的顶点,
为抛物线的顶点, ,
, ,
,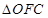 的面积分别记为
的面积分别记为 ,
, ,
, ,求证:
,求证: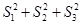 为定值.
为定值.