一同学家住在23层高楼的顶楼．他想研究一下电梯上升的运动过程．某天他乘电梯上楼时携带了一个质量为5kg的重物和一个量程足够大的台秤，他将重物放在台秤上．电梯从第1层开始启动，一直运动到第23层停止．在这个过程中，他记录了台秤在不同时段内的读数如下表所示．g取10m/s2，根据表格中的数据，求：
| 时间/s |
台秤示数/N |
| 电梯启动前 |
50.0 |
| 0～3.0 |
58.0 |
| 3.0～13.0 |
50.0 |
| 13.0～19.0 |
46.0 |
| 19.0以后 |
50.0 |
（1）电梯在最初加速阶段和最后减速阶段的加速度大小；
（2）电梯在中间阶段匀速上升的速度大小；
（3）该楼房平均每层楼的高度．
如图所示，一弹簧竖直悬挂气缸的活塞，使气缸悬空静止，活塞与气缸间无摩擦，缸壁导热性能良好。已知气缸重为G，活塞截面积为S，外界大气压强为P0，环境温度为T，活塞与筒底间的距离为d，当温度升高ΔT时，求（1）活塞与筒底间的距离变化量；（2）此过程中气体对外做的功。
如图甲所示，光滑绝缘水平桌面上直立一个单匝正方形导线框ABCD，线框的边长为
m、总电阻为
。在直角坐标系
中，有界匀强磁场区域的下边界与
轴重合，上边界满足曲线方程
（m），场强大小
。线框在沿轴正方向的拉力
作用下，以速度
水平向右做匀速直线运动，恰好拉出磁场。
（1）求线框中AD两端的最大电压；
（2）在图乙中画出运动过程上线框i-t图象，并估算磁场区域的面积；
（3）求线框在穿越整个磁场的过程中，拉力所做的功。
水平传送带被广泛地应用于机场和火车站，用于对旅客的行李进行安全检查。如图所示为一水平传送带装置示意图，绷紧的传送带AB始终保持v=1m/s的恒定速率运行。一质量为m=4kg的行李无初速度地放在A处，传送带对行李的滑动摩擦力使行李开始做匀加速直线运动，随后行李又以与传送带相等的速率做匀速直线运动。设行李与传送带间的动摩擦因数μ=0.1，AB间的距离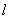
=2m，g取10 m/s2。
（1）求行李刚开始运动时所受的滑动摩擦力大小与加速度大小；
（2）求行李做匀加速直线运动的时间；
（3）如果提高传送带的运行速率，行李就能被较快地传送到B处。求行李从A处传送到B处的最短时间和传送带对应的最小运行速率。
如图所示，地面上放一木箱，质量为40kg，用与水平方向成370角，大小为100N的力推木箱，恰好使木箱匀速前进．若用大小为100N，方向与水平成370角的力斜向上方拉木箱，木箱加速运动(g取10m／s2，
，
))
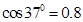求：（1）木箱与地面的动摩擦因素。
（2）木箱加速运动时的加速度大小。
一矿井深为125 m ，在井口每隔一定时间自由下落一个小球。当第11个小球刚从井口开始下落时，第1个小球恰好到达井底，求：
（1）相邻两个小球开始下落的时间间隔；
（2）这时第3个小球和第5个小球相隔的距离。（g="10" m/s2）