要求摩托车由静止开始在尽量短的时间内走完一段直道，然后驶入一段半圆形的弯道，但在弯道上行驶时车速不能太快，以免因离心作用而偏出车道，求摩托车在直道上行驶所用的最短时间．有关数据见表格.
| 启动加速度a1 |
4 m/s2 |
| 制动加速度a2 |
8 m/s2 |
| 弯道最大速度v2 |
20 m/s |
| 直道长度x |
218 m |
(10分)A物体做匀速直线运动，速度是1m/s，A出发后5s，B物体从同一地点从静止开始出发做匀加速直线运动，加速度是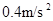
，且A、B运动方向相同，问：
⑴ B出发后几秒钟才能追上A？
⑵ A、B相遇前它们之间的最大距离是多少？
(12分)如图所示，斜面倾角为θ，木板A的质量为M，物块B的质量为m．绳的一端与B连接，另一端与固定在斜面上的挡板相连，绳与斜面平行．已知A与B间 的动摩擦因数为μ1，A与斜面间的动摩擦因数为μ2．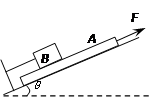
（１）若在沿斜面向上的力F作用下A正沿斜面向上匀速运动，求F的值．
（２）若将（１）中的力换成2F，求此时连接B的轻绳上的拉力大小．
(12分)如图所示，一轻质三角形框架B处悬挂一定滑轮（质量可忽略不计）。一体重为500N的人通过跨定滑轮的轻绳匀速提起一重为300N的物体。
（1）此时人对地面的压力是多大？
（2）斜杆BC，横杆AB所受的力是多大？
如图所示为一种获得高能粒子的装置，环形区域内存在垂直纸面向外、大小可调节的均匀磁场，质量为m，电量为＋q的粒子在环中做半径为R的圆周运动．A、B为两块中心开有小孔的极板，原来电势都为零，每当粒子飞经A板时，A板电势升高为＋U，B板电势仍保持为零，粒子在两极间电场中加速，每当粒子离开B板时，A板电势又降为零，粒子在电场一次次加速下动能不断增大，而绕行半径不变．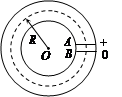
(1) 设t＝0时，粒子静止在A板小孔处，在电场作用下加速，并绕行第一圈．求粒子绕行n圈回到A板时获得的总动能En．
(2) 为使粒子始终保持在半径为R的圆轨道上运动，磁场必须周期性递增．求粒子绕行第n圈时的磁感应强度B．
(3) 求粒子绕行n圈所需的总时间tn（设极板间距远小于R）．
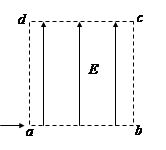
如图所示，边长为L的正方形区域abcd内存在着匀强电场。电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场，不计重力。若粒子从c点离开电场，求电场强度的大小和粒子离开电场时的动能？