如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置p(x,y).若初始位置为P0(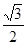 ,
, ),当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为( )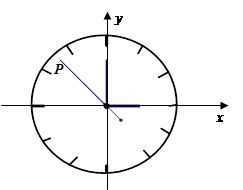
A.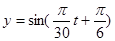 |
B.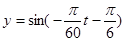 |
C. |
D. |
函数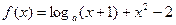 (
(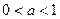 )的零点的个数为()
)的零点的个数为()
| A.3 | B.2 | C.1 | D.0 |
已知二次函数 和一次函数
和一次函数 ,则“
,则“ ”是“这两个函数的图象有两个不同交点”的()
”是“这两个函数的图象有两个不同交点”的()
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
集合A={( )½
)½ =
= |
| |},B={(
|},B={( )|
)| +
+ },C=A∩B,且集合C为单元素集合,则实数
},C=A∩B,且集合C为单元素集合,则实数 的取值范围是()
的取值范围是()
A.| |≤1 |≤1 |
B.| |>1或0<| |>1或0<| |< |<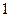 |
C. > >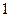 |
D. > > 或 或 < < |
如果奇函数f(x)在区间[3,7]上是增函数且最小值为5,则f(x)在区间[-7,-3]上是()
| A.增函数且最大值为-5 | B.增函数且最小值为-5 |
| C.减函数且最小值为-5 | D.减函数且最大值为-5 |
一种商品售价上涨2﹪后,又下降2﹪,则商品售价在两次调价后比原价()
| A.没有变化 | B.变高了 |
| C.变低了 | D.变高还是变低与原价有关 |