古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )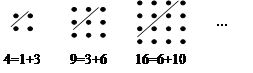
| A.13 = 3+10 | B.25 =" 9+16" |
| C.36 = 15+21 | D.49 = 18+31 |
今年我市计划扩大城区绿地面积,现有一块长方形绿地,它的短边长为60m,若将短边增长到长边相等(长边不变),使扩大后的棣地的形状是正方形,则扩大后的绿地面积比原来增加1600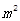 ,设扩大后的正方形绿地边长为xm,下面所列方程正确的是()
,设扩大后的正方形绿地边长为xm,下面所列方程正确的是()
| A.x(x-60)=1600 |
| B.x(x+60)=1600 |
| C.60(x+60)=1600 |
| D.60(x-60)=1600 |
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD、CD于点G,H,则下列结论错误的是()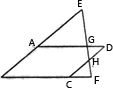
(A)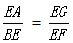 (B)
(B)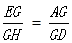 (C)
(C)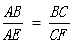 (D)
(D)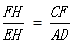
如图:某飞机在空中A处探测到它的正下方地平面上目标C,此时飞机飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角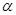 =
=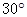 ,则飞机A与指挥台B的距离为()
,则飞机A与指挥台B的距离为()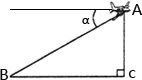
| A.1200m | B.1200 m m |
C.1200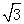 m m |
D.2400m |
如图所示的几何体是由五个小正方形体组合而成的,它的主视图是()

点A(-1, ),B(-2,
),B(-2, )在反比例函数
)在反比例函数 的图象上,则
的图象上,则 ,
, 的大小关系是()
的大小关系是()
A. > > |
B. = = |
C. < < |
D.不能确定 |