如图所示，在竖直面内有固定轨道ABCDE，其中BC是半径为R的四分之一圆弧轨道，AB（AB>R）是竖直轨道，CE是足够长的水平轨道，CD>R。AB与BC相切于B点，BC与CE相切于C点，轨道的AD段光滑，DE段粗糙且足够长。一根长为R的轻杆两端分别固定有质量均为m的相同小球P、Q（视为质点），将轻杆锁定在图示位置，此位置Q与B等高。现解除锁定释放轻杆，轻杆将沿轨道下滑，Q球经过D点后，沿轨道继续滑行了3R而停下。重力加速度为g。求：
（1）P球到达C点时的速度大小v1；
（2）两小球与DE段轨道间的动摩擦因数
；
（3）Q球到达C点时的速度大小v2。
(4分) 推导动能定理的表达式(要求做图写出必要的过程)
(10分)两个星体组成双星，它们在相互之间的万有引力作用下，绕连线上的某点做周期相同的匀速圆周运
动，现测得两星中心距离为R，其运动周期为T，求两星的总质量。
如图所示，水平光滑地面上停放着一辆小车，左侧靠在竖直墙壁上，小车的四分之一圆弧轨道AB是光滑的，在最低点B与水平轨道BC相切，BC的长度是圆弧半径的10倍，整个轨道处于同一竖直平面内。可视为质点的物块从A点正上方某处无初速下落，恰好落入小车圆弧轨道滑动，然后沿水平轨道滑行至轨道末端C处恰好没有滑出。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍，小车的质量是物块的3倍，不考虑空气阻力和物块落入圆弧轨道时的能量损失。求：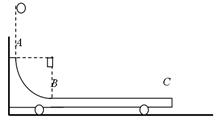
（1）物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍；
（2）物块与水平轨道BC间的动摩擦因数μ。
一静止的铀23292U（原子质量为232.0372u），放出一个
粒子（原子质量为4.00260u）后，衰变成22890Th（原子质量为228.0287u）。
（1）写出衰变方程；
（2）假设放出的结合能完全变成Th核和粒子的动能，求粒子的动能。
氢原子处于基态时，原子能量E1= -13.6eV，已知电子电量e =1.6×10-19C，电子质量m=0.91×10-30kg，氢的核外电子的第一条可能轨道的半径为r1=0.53×10-10m.
（1）若要使处于n=2的氢原子电离，至少要用频率多大的电磁波照射氢原子？
（2）氢原子核外电子的绕核运动可等效为一环形电流，则氢原子处于n=2的定态时，核外电子运动的等效电流多大？
（3）若已知钠的极限频率为6.00×1014Hz，今用一群处于n=4的激发态的氢原子发射的光谱照射钠，试通过计算说明有几条谱线可使钠发生光电效应？