如图,以矩形ABCD的顶点A为原点,AD所在的直线为x轴,AB所在的直线为y轴,建立平面直角坐标系.点D的坐标为(8,0),点B的坐标为(0,6),点F在对角线AC上运动(点F不与点A、C重合),过点F分别作x轴、y轴的垂线,垂足为G、E.设四边形BCFE的面积为S1,四边形CDGF的面积为S2,△AFG的面积为S3.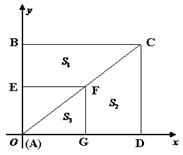
(1)试判断S1、S2,的关系,并加以证明;
(2)当S3:S1=1:3时,求点F的坐标;
(3)如图,在(2)的条件下,把△AEF沿对角线AC所在直线平移,得到△A’E’F’,且A’、F’两点始终在直线AC上,是否存在这样的点E’,使点E’到x轴的距离与到y轴的距离比是5:4.若存在,请求出点E’的坐标;若不存在,请说明理由.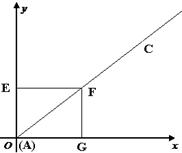
台风是夏季影响城市安全的重要因素之一.如图,坡上有一棵与水平面EF垂直的大树AB,被台风吹过后,大树倾斜并折断倒在山坡上,大树顶部B接触到坡面上的D点.已知山坡的坡角∠AEF=30°,量得∠BAC=45°,∠ADC=60°,AD=4米.
(1)求∠CAE的度数;(2)求这棵大树折断前的高度AB(结果精确到0.1米).
一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)
(1)填写表格中的空档;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
解方程:(1)x2-4x+1=0;(2)(x+1)(x+3)=x+1
计算:(1)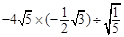 ;(2)
;(2)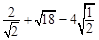
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm.如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
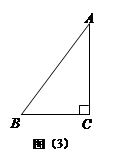
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)