从集合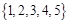 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组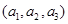 ,规定
,规定 .
.
(1)从所有的三元有序数组中任选一个,求它的所有元素之和等于10的概率
(2)定义三元有序数组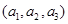 的“项标距离”为
的“项标距离”为 (其中
(其中 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=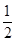 x上时,求直线AB的方程.
x上时,求直线AB的方程.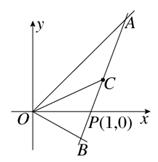
已知线段PQ两端点的坐标分别为(-1,1)、(2,2),若直线l:x+my+m=0与线段PQ有交点,求m的取值范围.
设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
已知点A(3,3),B(5,2)到直线l的距离相等,且直线l经过两直线l1:3x-y-1=0和l2:x+y-3=0的交点,求直线l的方程.
已知椭圆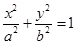
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,
, 是椭圆右准线上的一点,线段
是椭圆右准线上的一点,线段 的垂直平分线过点
的垂直平分线过点 .又直线
.又直线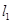 :
: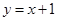 按向量
按向量 平移后的直线是
平移后的直线是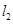 ,直线
,直线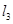 :
: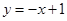 按向量
按向量 平移后的直线是
平移后的直线是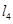 (其中
(其中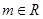 ).
).
(1)求椭圆的离心率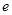 的取值范围.
的取值范围.
(2)当离心率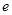 最小且
最小且 时,求椭圆的方程.
时,求椭圆的方程.
(3)若直线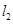 与
与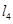 相交于(2)中所求得的椭圆内的一点
相交于(2)中所求得的椭圆内的一点 ,且
,且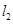 与这个椭圆交于
与这个椭圆交于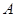 、
、 两点,
两点,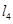 与这个椭圆交于
与这个椭圆交于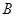 、
、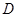 两点.求四边形ABCD面积
两点.求四边形ABCD面积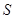 的取值范围.
的取值范围.