请认真阅读题意，并根据你的发现填空：
（1）将任何一组已知的勾股数中的每一个数都扩大为原来的正整数倍后，就得到一组新的勾股数，例如：3、4、5，我们把每一个数扩大为原来的2倍、3倍，则分别得到6、8、10和9、12、15，
若把每一个数都扩大为原来的12倍，就得到______________，
若把每一数都扩大为原来的n（n为正整数）倍，则得到_________________；
（2）对于任意一个大于1的奇数，存在着下列勾股数
若勾股数为3、4、5. 则有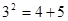
若勾股数为5、12、13， 则有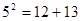
若勾股数为7、24、25， 则有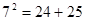
若勾股数为m（m为奇数）、n、______
则有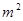
=2n+1，用m表示n=_______
当m=17时，n=_______，此时勾股数为_______________.
甲、乙两个袋中均有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标的数值分别为－7,－1,3，乙袋中的三张卡片上所标的数值分别为－2,1,6．先从甲袋中随机取出一张卡片，用x表示取出的卡片上标的数值，再从乙袋中随机取出一张卡片，用y表示取出的卡片上标的数值，把x、y分别作为点A的横坐标、纵坐标.
（1）用适当的方法写出点
的所有情况；
（2）求点A落在第二象限的概率.
为了解某市九年级学生学业考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段（A：50分；B：49-45分；C：44-40分；D：39-30分；E：29-0分）统计如下：
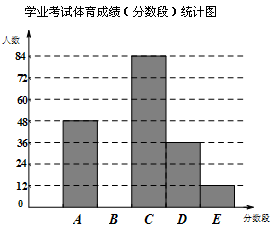
根据上面提供的信息，回答下列问题：
（1）在统计表中，a的值为 ________，b的值为______，并将统计图补充完整；
（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数．”请问：甲同学的体育成绩应在什么分数段内？（填相应分数段的字母）
（3）如果把成绩在40分以上（含40分）定为优秀，那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名？
解不等式组
并把解集在数轴上表示出来．
（1）计算：（）0 - （）-2 +
；
（2）解方程： - = 2．
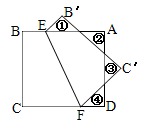
如图，正方形纸片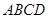
的边长为4，将其沿
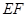折叠，则图中①②③④四个三角形的周长之和为.