如下图所示，在水平匀速运动的传送带的左端(P点)，轻放一质量为m＝1kg的物块，物块随传送带运动到A点后水平抛出，恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆弧轨道下滑．B、D为圆弧的两端点，其连线水平．已知圆弧半径R＝1.0m，圆弧对应的圆心角θ＝106°，轨道最低点为C，A点距水平面的高度h＝0.8m．(g取10m/s2，sin53°＝0.8，cos53°＝0.6)求：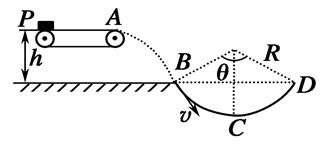
(1)物块离开A点时水平初速度的大小；
(2)物块经过C点时对轨道压力的大小；
(3)设物块与传送带间的动摩擦因数为0.3，传送带的速度为5m/s，求PA间的距离．
绝缘细绳的一端固定在天花板上，另一端连接着一个带负电的电量为q、质量为m的小球，当空间建立水平方向的匀强电场后，绳稳定处于与竖直方向成θ=600角的位置，如图所示。（1）求匀强电场的场强E；（2）若细绳长为L，让小球从θ=300的A
点释放，王明同学求解小球运动至某点的速度的过程如下：
据动能定理 -mgL（1—cos300）+qELsin300=
得：
你认为王明同学求的是最低点O还是θ=600的平衡位置处的速度，正确吗？请详细说明理由或求解过程。
如图所示，在光滑的水平面上有一块质量为2m的长木板A，木板左端放着一个质量为m的小木块B，A与B之间的动摩擦因数为μ，开始时，A和B一起以v0向右运
动，木板与墙发生碰撞的时间极短，碰后木板以原速率弹回，
求：（1）木板与小木块的共同速度大小并判断方向.
（2）由A开始反弹到A、B共同运动的过程中，B在A上滑行
的距离L。
（3）由B开始相对于A运动起，B相对于地面向右运动的最大距离s。
2008年9月25日，我国继“神舟”五号、六号载人飞船后又成功地发射了“神舟”七号载人飞船。如果把“神舟”七号载人飞船绕地球运行看作是同一轨道上的匀速圆周运动，宇航员测得自己绕地心做匀速圆周运动的周期为T、距地面的高度为H，且已知地球半径为R、地球表面重力加速度为g，万有引力恒量为G。你能计算出下面哪些物理量？能计算的量写出计算过程和结果，不能计算的量说明理由。
（1）地球的质量 ；
（2）飞船线速度的大小；
（3）飞船所需的向心力。
如
图所示，质量为m=2.0kg的小滑块，由静止开始从倾角
的固定的光滑斜面的顶端A滑至底端B，A点距离水平地面的高度h=5.0m，重力加速度g取10m/s2，求:
(1)滑块由A滑到B经历的时间；
(2)滑块由A滑到B的过程中支持力的冲量
(3) 滑块由A滑到B时的重力功率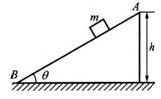
质量为8×107kg的列车，从某处开始进站并关闭发动机，只在恒定阻力作用下减速滑行．已知它开始滑行时的初速度为20m/s，当它滑行了300m时，速度减小到10m/s，接着又滑行了一段距离后刚好到达站台停下
，那么：
（1）关闭动力时列车的初动能为多大?
（2）列车受到的恒定阻力为多大?
（3）列车进站滑行的总时间为多大？