如图所示,一质点做简谐运动,先后以相同的速度依次通过A、B两点,历时1 s,质点通过B点后再经过1 s又第2次通过B点,在这2 s内质点通过的总路程为12 cm.则质点的振动周期和振幅分别为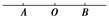
A.3 s,6 cm B.4 s,6 cm C.4 s,9 cm D.2 s,8 cm
有一外力作用在木块A上,将A、B挤压在竖直墙上静止,如图所示。下列关于对B木块判断中正确的是()
A.B木块总受到4个力, A对B的摩擦力为竖直向下
B.B木块总受到4个力, A对B的摩擦力为竖直向上
C.B木块总受到5个力, A对B的摩擦力为竖直向下
D.B木块总受到5个力, A对B的摩擦力为竖直向上
物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因数分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a与拉力F的关系如图所示,A、B两直线平行,则以下关系正确的是()
A.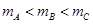 B.
B.
C. D.
D.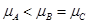
下列说法中正确的是()
| A.有力作用在物体上,物体才能运动;没有力作用在物体上,物体就要静止下来 |
| B.物体不受外力作用时,物体有惯性;当物体受外力作用时,惯性便消失 |
| C.物体做匀速直线运动或静止时有惯性,做其他运动时没有惯性 |
| D.一切物体都有惯性,与物体运动状态无关 |
如图所示,在一根水平的粗糙的直横梁上,套有两个质量均为m的铁环,两铁环系有等长的细绳,共同拴着质量为M的小球,两铁环与小球均保持静止。现使两铁环间距离增大少许,系统仍保持静止,则水平横梁对铁环的支持力N和摩擦力F将()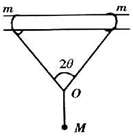
| A.N增大,F不变 | B.N增大,F增大 |
| C.N不变,F不变 | D.N不变,F增大 |
在探究力的合成的实验中,橡皮条的一端固定在P点,另一端被A、B两只弹簧测力计拉伸至O点,F1、F2分别表示A、B两只弹簧测力计的读数,如图所示.使弹簧测力计B从图示位置开始顺时针缓慢转动,在这过程中保持O点和弹簧测力计A的拉伸方向不变,则在整个过程中两弹簧测力计的读数F1、F2的变化是( )
A.F1减小,F2减小
B.F1减小,F2增大
C.F1减小,F2先增大后减小
D.F1减小,F2先减小后增大