已知两点 及
及 ,点
,点 在以
在以 、
、 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列.
(1)求椭圆 的方程;
的方程;
(2)如图,动直线 与椭圆
与椭圆 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线上的两点,且
是直线上的两点,且 ,
, . 求四边形
. 求四边形 面积
面积 的最大值.
的最大值.
已知矩阵
 ,A的一个特征值
,A的一个特征值 ,其对应的特征向量是
,其对应的特征向量是 .
.
(Ⅰ)求矩阵 ;
;
(Ⅱ)若向量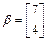 ,计算
,计算 的值.
的值.
已知函数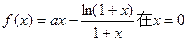 处取得极值.
处取得极值.
(1)求实数a的值,并判断 上的单调性;
上的单调性;
(2)若数列 满足
满足 ;
;
(3)在(2)的条件下,
记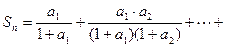

求证:
已知圆 ,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量
,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量 .
.
(1)求动点Q的轨迹E的方程;
(2)当 时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.
时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.
某工厂生产一种精密仪器,产品是否合格需先后经两道相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,经长期监测发现,该仪器第一道工序检查合格的概率为 ,第二道工序检查合格的概率为
,第二道工序检查合格的概率为 .已知该厂每月生为3台这种仪器.
.已知该厂每月生为3台这种仪器.
(1)求每生产一台合格仪器的概率;
(2)用 表示每月生产合格仪器的台数,求
表示每月生产合格仪器的台数,求 的分布列和数学期望;
的分布列和数学期望;
(3)若生产一台仪器合格可盈利10万元,不合格要亏损3万元,求该厂每月的期望盈利额.
三棱锥P—ABC中,△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥平面ABC,D、E分别为AB、PB的中点.
(1)求证:AC⊥PD;
(2)求二面角E—AC—B的正切值;
|
(3)求三棱锥P—CDE与三棱锥P—ABC的体积之比.