已知函数 ,若关于
,若关于 的方程
的方程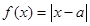 有三个不同的实根,则实数
有三个不同的实根,则实数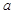 的取值范围是( )
的取值范围是( )
A.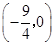 |
B. |
C. |
D. |
已知 为原点,双曲线
为原点,双曲线 上有一点
上有一点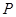 ,过
,过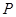 两条渐近线的平行线,且与两渐近线的交点分别为
两条渐近线的平行线,且与两渐近线的交点分别为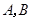 ,平行四边形
,平行四边形 的面积为
的面积为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.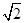 |
B. |
C. |
D.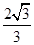 |
将一张边长为6 cm的纸片按如图1所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置,若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是( )
A. |
B. |
C. |
D.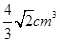 |
已知 为区域
为区域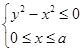 内的任意一点,当该区域的面积为
内的任意一点,当该区域的面积为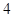 时,
时,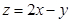 的最大值是( )
的最大值是( )
A.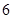 |
B.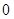 |
C.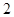 |
D. |
已知非零向量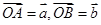 ,且
,且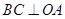 ,
,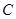 为垂足,若
为垂足,若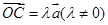 ,则
,则 等于( )
等于( )
A.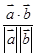 |
B.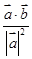 |
C.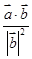 |
D.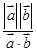 |