已知函数 (
(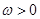 ),相邻两对称轴之间的距离为
),相邻两对称轴之间的距离为 .
.
(1)求函数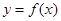 的解析式;
的解析式;
(2)把函数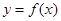 的图象向右平移
的图象向右平移 个单位,再纵坐标不变横坐标缩短到原来的
个单位,再纵坐标不变横坐标缩短到原来的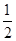 后得到函数
后得到函数 的图象,当
的图象,当 时,求函数
时,求函数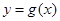 的单调递增区间.
的单调递增区间.
已知函数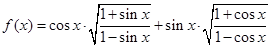
(1)当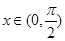 时,化简
时,化简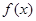 的解析式并求
的解析式并求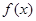 的对称轴和对称中心;
的对称轴和对称中心;
(2)当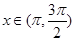 时,求函数
时,求函数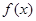 的值域.
的值域.
求下列函数定义域:(1) ;(2)
;(2)
已知矩形 中,
中, ,
, ,
, ,
, 分别在
分别在 ,
, 上,且
上,且 ,
, ,沿
,沿 将四边形
将四边形 折成四边形
折成四边形 ,使点
,使点 在平面
在平面 上的射影
上的射影 在直线
在直线 上.
上.
(1)求证: 平面
平面 ;
;
(2)求二面角 的大小.
的大小.
如图,边长为2的正方形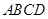 绕
绕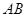 边所在直线旋转一定的角度(小于
边所在直线旋转一定的角度(小于 )到
)到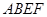 的位置.
的位置.
(1)若 ,求三棱锥
,求三棱锥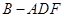 的外接球的表面积;
的外接球的表面积;
(2)若 为线段
为线段 上异于
上异于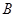 ,
,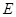 的点,
的点,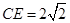 ,设直线
,设直线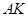 与平面
与平面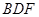 所成角为
所成角为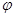 ,当
,当 时,求
时,求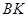 的取值范围.
的取值范围.