如下图所示,竖直平面(纸面)内有直角坐标系,轴沿水平方向。在≤O的区域内存在方向垂直于纸面向里,磁感应强度大小为的匀强磁场。在第二象限紧贴轴固定放置长为、表面粗糙的不带电绝缘平板,平板平行于轴且与轴相距。在第一象限内的某区域存在方向相互垂直的匀强磁场(磁感应强度大小为、方向垂直于纸面向外)和匀强电场(图中未画出)。一质量为、不带电的小球从平板下侧点沿轴正向抛出;另一质量也为、带电量为的小球从点紧贴平板沿轴正向运动,变为匀速运动后从轴上的点进入电磁场区域做匀速圆周运动,经圆周离开电磁场区域,沿轴负方向运动,然后从轴上的点进入第四象限。小球相遇在第四象限的某一点,且竖直方向速度相同。设运动过程中小球电量不变,小球和始终在纸面内运动且均看作质点,重力加速度为。求:

(1)匀强电场的场强大小,并判断P球所带电荷的正负;
(2)小球的抛出速度的取值范围;
(3)是的多少倍?
我国国防科技工业局在2012年7月30日宣布,“嫦娥三号”将于2013年下半年择机发射。我国已成功发射了“嫦娥二号”探月卫星,已知该卫星在环月圆轨道绕行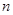 圈所用的时间为
圈所用的时间为 ,月球半径为
,月球半径为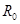 ,月球表面的重力加速度为
,月球表面的重力加速度为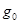 .
.
(1)请推导出“嫦娥二号”卫星离月球表面高度的表达式;
(2)地球和月球的半径之比为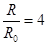 、表面重力加速度之比为
、表面重力加速度之比为 ,试求地球和月球的密度之比.
,试求地球和月球的密度之比.
有两列简谐横波a、b在同一媒质中沿 轴正方向传播,波速均为
轴正方向传播,波速均为 .在t=0时,两列波的波峰正好在
.在t=0时,两列波的波峰正好在 处重合,如图所示.
处重合,如图所示.
①求两列波的周期 和
和 。②求t=0时,两列波的波峰重合处的所有位置。
。②求t=0时,两列波的波峰重合处的所有位置。
一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的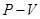 图象如图所示,已知该气体在状态A时的温度为
图象如图所示,已知该气体在状态A时的温度为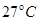 .则:
.则: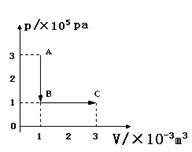
①该气体在状态B、C时的温度分别为多少℃? ②该气体从状态A到状态C的过程中内能的变化量是多大?
如图所示,在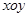 平面内的第一象限内存在沿
平面内的第一象限内存在沿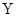 轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度
轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度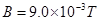 ,有一质量为
,有一质量为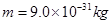 ,电量为
,电量为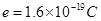 的电子以
的电子以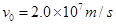 的速度从
的速度从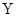 轴的
轴的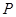 点(0,
点(0,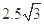 cm)沿
cm)沿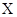 轴正方向射入第一象限,偏转后从
轴正方向射入第一象限,偏转后从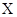 轴的
轴的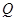 点射入第四象限,方向与
点射入第四象限,方向与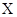 轴成
轴成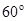 角,在磁场中偏转后又回到
角,在磁场中偏转后又回到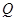 点,方向与
点,方向与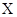 轴也成
轴也成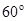 角;不计电子重力.求:
角;不计电子重力.求: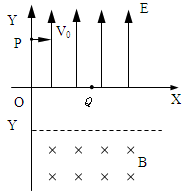
(1)OQ之间的距离及电子通过Q点的速度大小.
(2)若在第四象限内的磁场的边界为直线边界,即在虚线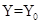 的下方有磁场,如图中所示,求
的下方有磁场,如图中所示,求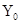 的坐标.
的坐标.
(3)若在第四象限内的磁场为圆形边界的磁场,圆形边界的磁场的圆心坐标的范围.
如图所示,两根足够长的固定平行金属导轨位于同一水平面内,导轨间的距离为 ,导轨上横放着两根导体棒ab和cd.设两根导体棒的质量皆为
,导轨上横放着两根导体棒ab和cd.设两根导体棒的质量皆为 ,电阻皆为
,电阻皆为 ,导轨光滑且电阻不计,在整个导轨平面内都有竖直向上的匀强磁场,磁感强度为
,导轨光滑且电阻不计,在整个导轨平面内都有竖直向上的匀强磁场,磁感强度为 .开始时ab和cd两导体棒有方向相反的水平初速,初速大小分别为
.开始时ab和cd两导体棒有方向相反的水平初速,初速大小分别为 和
和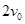 ,求:
,求:
(1)从开始到最终稳定回路中产生的焦耳热.
(2)当ab棒的速度大小变为 ,回路中消耗的电功率的可能值.
,回路中消耗的电功率的可能值.