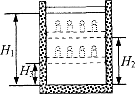
如图,柱形容器内用不漏气的轻质绝热活塞封闭一定量的理想气体,容器外包裹保温材料。开始时活塞至容器底部的高度为,容器内气体温度与外界温度相等。在活塞上逐步加上多个砝码后,活塞下降到距容器底部处,气体温度升高了;然后取走容器外的保温材料,活塞位置继续下降,最后静止于距容器底部处:已知大气压强为。求:气体最后的压强与温度。
质量m = 3kg的物体,在水平力F = 6N的作用下,在光滑水平面上从静止开始运动,运动时间t = 3s,试求:
(1)力F在t = 3s内对物体所做的功;
(2)力F在t = 3s内对物体做功的平均功率;
(3)在3s末力F对物体做功的瞬时功率.
一宇航员在某未知星球的表面上做平抛运动实验:在离地面h高处让小
球以v0的初速度水平抛出,他测出小球落地点与抛出点的水平距离为x,又已知该
星球的半径为R,己知万有引力常量为G,求:
(1)、该星球表面的重力加速度g
(2)、该星球的质量M
(3)、该星球的第一宇宙速度v
(最后结果必须用题中己知物理量表示)
如图所示,AB是竖直面内的四分之一圆弧光滑轨道,下端B与水平直轨道相切。一个小物块自A点由静止开始沿轨道下滑,已知轨道半径为R=0.2m,小物块的质量为m=0.1kg,小物块与水平面间的动摩擦因素μ=0.5,取g=10m/s2。求:
(1)小物块到达B点的速度大小
(2)小物块在B点时受圆弧轨道的支持力
(3)小物块在水平面上滑动的最大距离
质量均为m的物体A和B分别系在一根不计质量的细绳两端,绳子跨过固定在倾角为30°的光滑斜面顶端的定滑轮上,斜面固定在水平地面上。开始时把物体B拉到斜面底端,这时物体A离地面的高度为0.8m,如图所示。若摩擦力均不计,从静止开始放手让它们运动,取g=10m/s2。求:
(1)物体A着地时的速度
(2)物体A着地后物体B沿斜面上滑的最大距离
(8分)如图所示,飞机离地面高度为H=500m,飞机的水平飞行速度为v1=100m/s,追击一辆速度为v2=20m/s同向行驶的汽车,欲使炸弹击中汽车,飞机应在距离汽车的水平距离多远处投弹?(不考虑空气阻力,g取10m/s2。)