设
是已知的平面向量且
,关于向量
的分解,有如下四个命题:
①给定向量
,总存在向量
,使
;
②给定向量
和
,总存在实数
和
,使
;
③给定单位向量
和正数
,总存在单位向量
和实数
,使
;
④给定正数
和
,总存在单位向量
和单位向量
,使
;
上述命题中的向量
,
和
在同一平面内且两两不共线,则真命题的个数是()
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
已知集合 ,则如图所示韦恩图中的阴影部分所表示的集合为
,则如图所示韦恩图中的阴影部分所表示的集合为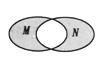
A.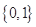 |
B. |
C.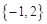 |
D. |
如图是函数 在区间上
在区间上 的图像,为了得到这个函数的图象,只要将
的图像,为了得到这个函数的图象,只要将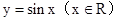 的图象上所有的点
的图象上所有的点
A.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的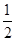 倍,纵坐标不变 倍,纵坐标不变 |
B.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的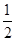 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
若△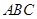 的三个内角满足
的三个内角满足 ,则△
,则△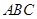
| A.一定是锐角三角形 |
| B.一定是直角三角形 |
| C.一定是钝角三角形 |
| D.可能是锐角三角形,也可能是钝角三角形 |
下列程序的运算结果为
| A.20 | B.15 | C.10 | D.5 |
设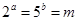 ,且
,且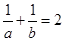 ,则
,则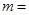
A.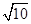 |
B.10 | C.20 | D.100 |