如图,已知双曲线
,曲线
,
是平面内一点,若存在过点
的直线与
都有公共点,则称
为"
型点"

(1)在正确证明
的左焦点是"
型点"时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线
与
有公共点,求证
,进而证明原点不是"
型点";
(3)求证:圆
内的点都不是"
型点"
设函数 则不等式
则不等式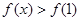 的解集____________
的解集____________
若不等式 对任意的实数
对任意的实数 恒成立,则实数
恒成立,则实数 的取值范围是.
的取值范围是.
如图所示,在一个边长为1的正方形AOBC内,曲线 和曲线
和曲线 围成一个叶形图(阴影部分),向正方形AOBC内随机投一点,该点落在正方形AOBC内任何一点是等可能的,则所投的点落在叶形图内部的概率为__________.
围成一个叶形图(阴影部分),向正方形AOBC内随机投一点,该点落在正方形AOBC内任何一点是等可能的,则所投的点落在叶形图内部的概率为__________.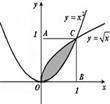
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: .由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元.
.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加____________万元.
某新型企业随市场竞争加剧,为获取更大利润,企业须不断加大投资,若预计年利润率低于10%时,则该企业就考虑转型.下表显示的是某企业几年来年利润 (百万)与年投资成本
(百万)与年投资成本 (百万)变化的一组数据.
(百万)变化的一组数据.
| 年份 |
2008 |
2009 |
2010 |
2011 |
… |
| 投资成本x |
3 |
5 |
9 |
17 |
… |
| 年利润y |
1 |
2 |
3 |
4 |
… |
请你就以下4个函数模型



其中以下说法
A.年投资成本与年利润正相关
B.选择其适合的函数模型是
C.若要使企业利润超过6百万,则该企业考虑转型.
你认为正确的是(把你认为正确的都填上)