某市举行一次数学新课程骨干培训活动,共邀请15名使用不同版本教材的数学教师,具体情况数据如下表所示:
| 版本 |
人教A版 |
人教B版 |
||
| 性别 |
男教师 |
女教师 |
男教师 |
女教师 |
| 人数 |
6 |
 |
4 |
 |
现从这15名教师中随机选出2名,则2人恰好是教不同版本的女教师的概率是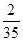 .且
.且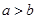 .
.
(1)求实数 ,
, 的值
的值
(2)培训活动现随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为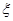 ,求随机变量
,求随机变量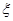 的分布列和数学期望
的分布列和数学期望 .
.
已知 为复数,
为复数,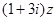 为纯虚数,
为纯虚数, ,且
,且 ,求
,求 .
.
对于在区间 上有意义的两个函数
上有意义的两个函数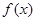 和
和 ,如果对于任意的
,如果对于任意的 ,都有
,都有 ,则称
,则称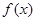 与
与 在区间
在区间 上是接近的两个函数,否则称它们在
上是接近的两个函数,否则称它们在 上是非接近的两个函数。现有两个函数
上是非接近的两个函数。现有两个函数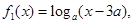 ,
,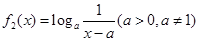 ,且
,且 与
与 在
在 都有意义.
都有意义.
(1)求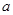 的取值范围;
的取值范围;
(2)讨论 与
与 在区间
在区间 上是否是接近的两个函数.
上是否是接近的两个函数.
下图是一个二次函数 的图象.写出
的图象.写出 的解集;
的解集;
(2)求这个二次函数的解析式;
(3)当实数 在何范围内变化时,
在何范围内变化时,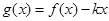 在区间
在区间  上是单调函数.
上是单调函数.
已知二次函数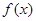 的最小值为1,且
的最小值为1,且 .
.
(1)求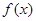 的解析式;
的解析式;
(2)若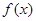 在区间
在区间 上不单调,求实数
上不单调,求实数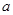 的取值范围;
的取值范围;
(3)在区间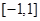 上,
上,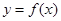 的图像恒在
的图像恒在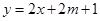 的图像上方,试确定实数
的图像上方,试确定实数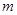 的取值范围.
的取值范围.
已知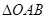 中,点
中,点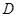 在线段
在线段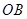 上,且
上,且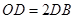 ,延长
,延长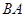 到
到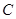 ,使
,使 .设
.设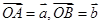 .
.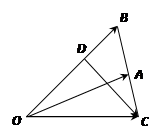
(1)用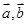 表示向量
表示向量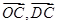 ;
;
(2)若向量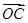 与
与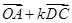 共线,求
共线,求 的值.
的值.