已知各项均不相等的等差数列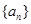 的前三项和为18,
的前三项和为18, 是一个与
是一个与 无关的常数,若
无关的常数,若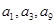 恰为等比数列
恰为等比数列 的前三项,
的前三项,
(1)求 的通项公式.
的通项公式.
(2)记数列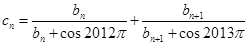 ,
,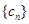 的前三
的前三 项和为
项和为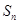 ,求证:
,求证: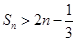
(本大题满分12分)
已知数列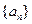 ,
,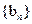 的通项公式分别为
的通项公式分别为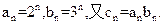
(I)求证数列{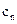 }是等比数列;
}是等比数列;
(II)求数列{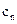 }的前n项和为
}的前n项和为 。
。
(本大题满分10分)
已知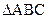 的顶点坐标分别为A(-1,1),B(2,7),C(-4,5)。
的顶点坐标分别为A(-1,1),B(2,7),C(-4,5)。
求AB边上的高CD所在的直线方程。
已知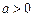 ,
,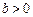 且
且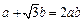 ,求
,求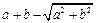 的最大值.
的最大值.
在平面直角坐标系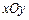 中,已知圆
中,已知圆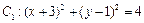 和圆
和圆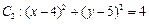 .
.
(1)若直线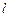 过点
过点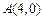 ,且被圆
,且被圆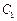 截得的弦长为
截得的弦长为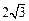 ,求直线
,求直线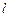 的方程;
的方程;
(2)设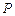 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点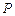 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线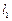 和
和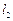 ,它们分别与圆
,它们分别与圆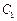 和圆
和圆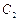 相交,且直线
相交,且直线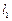 被圆
被圆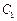 截得的弦长与直线
截得的弦长与直线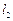 被圆
被圆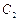 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点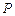 的坐标.
的坐标.
如图,在五面体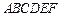 中,
中,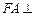 平面
平面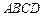 ,
,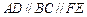 ,
,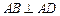 ,
,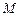 为
为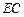 的中点,
的中点,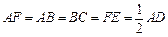 .
.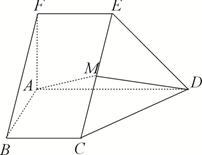
(1)求异面直线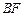 与
与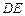 所成角的大小;
所成角的大小;
(2)证明:平面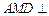 平面
平面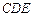 ;
;
(3)求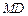 与平面
与平面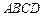 所成角的正弦值.
所成角的正弦值.