已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G。有关同步卫星,下列表述正确的是 ( )
A.卫星距离地面的高度为 |
| B.卫星的运行速度小于第一宇宙速度 |
| C.卫星运行时受到的向心力大小为GMm/R2 |
| D.卫星运行的向心加速度小于地球表面的重力加速度 |
如图中的圆a、b、c,其圆心均在地球的自转轴线上,对卫星环绕地球做匀速圆周运动而言()
| A.卫星的轨道只可能为a |
| B.卫星的轨道可能为b |
| C.卫星的轨道可能为c |
| D.同步卫星的轨道一定为b |
假设人造地球卫星做匀速圆周运动,当它的轨道半径增大到原来的2倍时()
| A.根据F=mω2r,卫星受到的向心力增为原来的2倍 |
B.根据F=m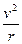 ,卫星受到的向心力减为原来的 ,卫星受到的向心力减为原来的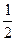 |
C.根据F=G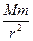 ,卫星受到的向心力减为原来的 ,卫星受到的向心力减为原来的 |
| D.根据F=mg,卫星受到的向心力保持不变 |
组成星球的物质是靠引力吸引在一起的,这样的星球有一个最大的自转速率,如果超过了该速率,星球的万有引力将不足以维持其赤道附近的物体做匀速圆周运动.由此可以得到半径为R、密度为ρ、质量为M且均匀分布的星球的最小自转周期T.运载赤道则下列表达式中正确的是()
A.T=2π |
B.T=2π |
C.T=  |
D.T= |
如图所示,在圆轨道上运行的国际空间站里,一宇航员A静止(相对空间舱)“站”在舱内朝向地球一侧的“地面”B上.则下列说法正确的是()
| A.宇航员A不受重力作用 |
| B.宇航员A所受重力与他在该位置所受的万有引力相等 |
| C.宇航员A与“地面”B之间无弹力作用 |
| D.若宇航员A将手中一小球无初速(相对空间舱)释放,该小球将落到“地面”B上 |
最近,科学家在望远镜中看到太阳系外某一恒星有一行星,并测得它围绕该恒星运行一周所用的时间为1 200年,它与该恒星的距离为地球到太阳距离的100倍.假定该行星绕恒星运行的轨道和地球绕太阳运行的轨道都是圆周,仅利用以上两个数据可以求出的量有()
| A.恒星质量与太阳质量之比 |
| B.恒星密度与太阳密度之比 |
| C.行星质量与地球质量之比 |
| D.行星运行速度与地球公转速度之比 |