推理填空:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD。理由如下:
∵ ∠1 =∠2(已知),且∠1 =∠4( ),
∴ ∠2 =∠4(等量代换),
∴ CE∥BF( ).
∴ ∠ =∠3( ).
又∵ ∠B =∠C(已知),
∴ ∠3 =∠B(等量代换),
∴ AB∥CD( ).
已知△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD与BE相交于点F.求证:△ABE≌△CAD.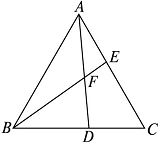
先化简,再求值: ¸
¸
 ,其中
,其中
解方程: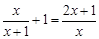 .
.
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.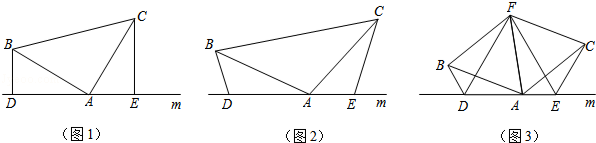
如图,四边形ABCD是正方形,BE⊥BF, BE=BF,EF与BC交于点G.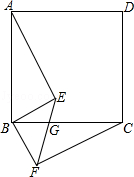
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.