如图,直线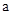 ,
, 被直线
被直线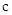 所截,若
所截,若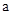 ∥
∥ ,∠1=40°,∠2=70°,则∠3= 度
,∠1=40°,∠2=70°,则∠3= 度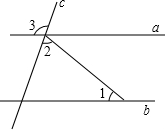
如果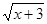 =2,那么(x+3)2=______ ;
=2,那么(x+3)2=______ ;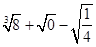 =
=
在下面的加法竖式中,如果不同的汉字代表不同的数字。使得算式成立,那么四位数
“华杯初赛”的最小值是。
公交车的线路号是由数字显示器显示的三位数,其中每个数字是由横竖放置的七支荧光管
显示,如下图所示:
由于坏了一支荧光管,某公交线路号变成“351”。若该线路号恰好等于两个不同的两位质数
的积,则正确的线路是路。
老师问A、B、C、D、E五位学生:“昨天你们有几个人玩过游戏?”他们的回答分别为A:
没有人;B:一个人;C:二个人;D;三个人;E:四个人。老师知道:他们之中有人玩过
游戏,也有人没有玩过游戏。若没有玩过游戏的人说的是真话,那么他们5个人中有个
人玩过游戏。
对整数按以下方法进行加密;每个数字的数字变为与7乘积的个位数字,再把每个数位上的
数字a变为10-a。如果一个数按照上面的方法加密后为473392,则该数为。