某校为了进一步开展“阳光体育”活动，购买了一批乒乓球拍和羽毛球拍，已知一副羽毛球拍比一副乒乓球拍费贵20元，购买羽毛球拍的费用比购买乒乓球拍的2000元要多，多出部分能购买25副乒乓球拍。
（1）若每副乒乓球拍的价格为x元,请你用含x的代数式表示该校购买这批乒乓球拍和羽毛球拍的总费用。
（2）若购买的两种球拍数一样，求x。
在一次投篮比赛中，甲、乙两人共进行五轮比赛，每轮各投10个球，他们每轮投中的球数如下表：
| 轮次 |
一 |
二 |
三 |
四 |
五 |
| 甲投中（个） |
6 |
8 |
7 |
5 |
9 |
| 乙投中（个） |
7 |
8 |
6 |
7 |
7 |
请你计算甲、乙两人投篮的平均数.
从统计学的角度考虑，通过计算，你认为在比赛中甲、乙两人谁的发挥更稳定些？
若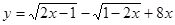
，求
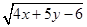的平方根.
(1)计算：
÷
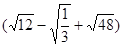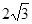
(2) 解方程：
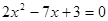
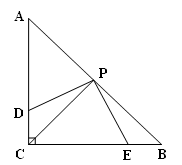
如图，在Rt△ABC中，
∠C=90°，AC=BC，点P是斜边中点，将一个等腰直角三角板绕点P旋转，三角板的两条直角边与AC、BC交于点D、E，连结PC．（1）求证：PC平分∠ACB ；
（2）图中有个等腰直角三角形，分别是；
（3）求证：PD=PE．
如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点 ，旋转角度是
度；（2）若连结EF，则△AEF是 三角形；
（3）若四边形AECF的面积为25，DE=2，求AE的长．
