我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”。如图1，四边形ABCD即为“准等腰梯形”。其中∠B=∠C。
（1）在图1所示的“准等腰梯形”ABCD中，选择合适的一个顶点引一条直线将四边形ABCD分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形（画出一种示意图即可）。
（2）如图2，在“准等腰梯形”ABCD中，∠B=∠C，E为边BC上一点，若AB∥DE，AE∥DC，求证：
（3）在由不平行于BC的直线截ΔPBC所得的四边形ABCD中，∠BAD与∠ADC的平分线交于点E，若EB=EC，请问当点E在四边形ABCD内部时（即图3所示情形），四边形ABCD是不是“准等腰梯形”，为什么？若点E不在四边形ABCD内部时，情况又将如何？写出你的结论（不必说明理由）
永川区某中学为了营造良好的文化氛围，学校决定在学校的一段文化墙上制作一幅永久性的标语，为此，在文化墙上特别做了一个长1640cm的长方形横标框，铺红色衬底．为了使制作时方便、制作出来的标语美观，对有关数据作了如下规定：边空:字宽:字距=6:9:2，如图所示．
根据这个规定，若这幅标语名称的字数为14，则边空、字宽、字距各是多少?
如图，AB为直线，OC是∠AOD的平分线，OE在∠BOD内，DOE=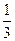
∠BOD,
∠COE=72°，求∠EOB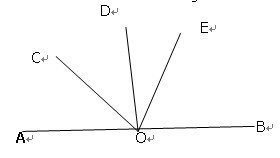
用棋子摆出下列一组图形：
（1）、填写下表：
| 图形编号 |
1 |
2 |
3 |
4 |
5 |
6 |
| 图中棋子数 |
5 |
8 |
11 |
14 |
（2）、照这样的方式摆下去，写出摆第
个图形所需棋子的枚数；
（3）、其中某一图形可能共有2011枚棋子吗？若不可能，请说明理由；若可能，请你求出是第几个图形
(1) 已知x=-3是关于x的方程2k-x-k(x+4)=5的解,求k的值.
（2）在(1)的条件下，已知线段AB=12cm，点C是直线AB上一点，且AC:BC=1:k，若点D是AC的中点，求线段CD的长.
先化简,后求值
3
b－〔2a
－2（ab－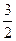
b）+ab〕+3a,其中a=3，b=
.