设函数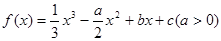 ,曲线
,曲线 在点
在点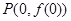 处的切线方程为
处的切线方程为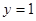
(1)确定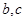 的值
的值
(2)若过点(0,2)可做曲线 的三条不同切线,求
的三条不同切线,求 的取值范围
的取值范围
(3)设曲线 在点
在点 处的切线都过点(0,2),证明:当
处的切线都过点(0,2),证明:当 时,
时,
设函数 分别在
分别在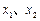 处取得极小值、极大值.
处取得极小值、极大值.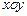 平面上点
平面上点 的坐标分别为
的坐标分别为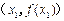 、
、 ,该平面上动点
,该平面上动点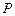 满足
满足 ,点
,点 是点
是点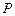 关于直线
关于直线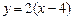 的对称点,.求
的对称点,.求
(Ⅰ)求点 的坐标;
的坐标;
(Ⅱ)求动点 的轨迹方程.
的轨迹方程.
设函数 在
在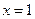 及
及 时取得极值.
时取得极值.
(1)求a、b的值;
(2)若对于任意的 ,都有
,都有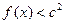 成立,求c的取值范围.
成立,求c的取值范围.
用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
已知椭圆方程为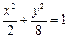 ,射线
,射线 与椭圆的交点为
与椭圆的交点为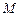 ,过
,过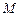 作倾斜角互补的两条直线,分别与椭圆于
作倾斜角互补的两条直线,分别与椭圆于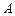 、
、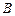 两点(异于
两点(异于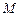 ).
).
(1)求证:直线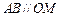 ;
;
(2)求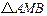 面积的最大值.
面积的最大值.
已知函数f(t)=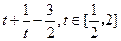
(1)求f(t)的值域G;
(2)若对于G内的所有实数x,不等式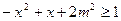 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.