如图，在平面直角坐标系中，二次函数
的图象与
轴交于A（
，0），B（2，0），且与
轴交于点C.
（1）求该抛物线的解析式，并判断△ABC的形状；
（2）点P是x轴下方的抛物线上一动点， 连接PO，PC，
并把△POC沿CO翻折，得到四边形
，求出使四边形为菱形的点P的坐标；
(3) 在此抛物线上是否存在点Q，使得以A，C，B，Q四点为顶点的四边形是直角梯形？若存在, 求出Q点的坐标；若不存在，说明理由.
已知：如图，在▱ABCD中，E、F是对角线AC上的两点，且AE=CF．求证：四边形BFDE是平行四边形．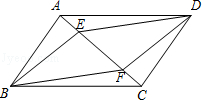
为了从甲、乙两人中选拔一人参加射击比赛，现对他们的射击成绩进行了测试，5次打靶命中的环数如右：甲：8，7，10，7，8； 乙：9，5，10，9，7．
（1）将下表填写完整；
| 平 均 数 |
方 差 |
|
| 甲 |
||
| 乙 |
3．2 |
（2）若你是教练，根据以上信息，你会选择谁参加射击比赛，理由是什么？
为保护学生视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为ycm，椅子的高度为xcm，则y是x的一次函数，下表列出两套符合条件的课桌椅的高度．
| 第一套 |
第二套 |
|
| 椅子高度x（cm） |
42 |
38 |
| 课桌高度y（cm） |
74 |
70 |
（1）请确定课桌高度与椅子高度的函数关系式；
（2）现有一张高80cm的课桌和一张高为43cm的椅子，它们是否配套？为什么？
已知反比例函数y=
的图象经过点P（1，6）．
（1）求k的值；
（2）若点M（﹣2，m），N（﹣1，n）都在该反比例函数的图象上，试比较m，n的大小．
某学校设立学生奖学金时规定：综合成绩最高者得一等奖，综合成绩包括体育成绩、德育成绩、学习成绩三项，这三项成绩分别按1：3：6的比例计入综合成绩．小明、小亮两位同学入围测评，他们的体育成绩、德育成绩、学习成绩如下表．请你通过计算他们的综合成绩，判断谁能拿到一等奖？
| 体育成绩 |
德育成绩 |
学习成绩 |
|
| 小明 |
96 |
94 |
90 |
| 小亮 |
90 |
93 |
92 |