如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。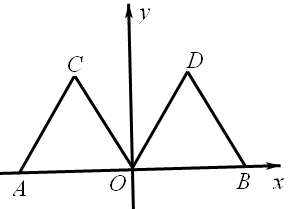
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△OBD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是 度;
(2)连接AD,交OC于点E,求∠AEO的度数。
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).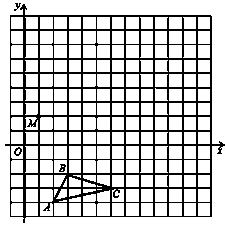
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2∶1.
(3)请写出(2)中放大后的△A2B2C2中A2B2边的中点P的坐标..
为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计该市直机关600户家庭中月平均用水量不超过12吨的约有多少户?
若关于 的一元二次方程
的一元二次方程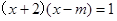 .
.
(1)求证:无论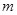 取何实数,原方程总有两个不相等的实数根;
取何实数,原方程总有两个不相等的实数根;
(2)若原方程有一个根为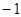 ,求
,求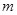 的值和此方程的另一个根.
的值和此方程的另一个根.
如图,某小区有一块长为24米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为72米2,两块绿地之间及周边留有宽度相等的人行通道,求人行道的宽度.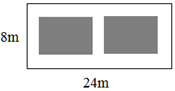
先化简,再求值: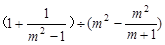 ,其中
,其中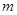 是方程
是方程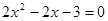 的根.
的根.