已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O 上运动(不与点B重合),连接CD,且CD=OA.
(1)当OC=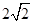 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;
(2)当OC>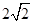 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
①当D为CE中点时,求△ACE的周长;
②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE·ED的值;若不存在,请说明理由。
已知 是
是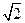 的小数部分,求
的小数部分,求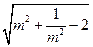 的值
的值
直线AB: 分别与x、y轴交于A
分别与x、y轴交于A  、B两点,过点B的直线交x轴负半轴于C,且
、B两点,过点B的直线交x轴负半轴于C,且 ;
;
(1)求直线BC的解析式;
(2)直线EF: (
( )交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得
)交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由?
的值;若不存在,说明理由?
(3)P为A点右侧x轴上的一动点,以P为直角顶点、BP为腰在第一象限内作等腰直角三角形△BPQ,连结QA并延长交y轴于点K。当P点运动时,K点的位置是否发生变化?如果不变请求出它的坐标;如果变化,请说明理由。
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为 、
、 (km),
(km), 、
、 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为 km, ;
;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)若两船的距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
⑴如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
⑵如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多可获得多少利润?此时如何分配加工时间?
如图:已知直线L的解析式为y=-3x+3,且L与x轴交于点D,直线m经过点A、B,直线L、m交于点C。
(1)、求直线m的解析式;
(2)、在直线m上存在异于点C的点P,使得△ADP与△ADC的面积相等,请求出点C的坐标