（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=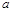
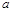,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.
2(2xy2-
y2)-(4xy2+
y2-x2y)-
y2，其中x=
，y=-
（1）
；
（2）
.
如图11，正方形ABCD的边长为5，点F为正方形ABCD内的点，△BFC经逆时针旋转后能与△BEA重合.
（1）旋转中心是哪一点？旋转了多少度？
（2）判断△BEF是怎样的三角形？并说明理由；
（3）若BE=3，FC=4，说明AE∥BF.
如图10，在梯形ABCD中，AD∥BC，AB
= DC=1，BD平分∠ABC，BD⊥CD.
（1）求：① ∠BAD的度数；② BD的长；
（2）延长BC至点E，使C
E=CD，说明△DBE是等腰三角形
如图9，在正方形网格中每个小正方形的边长都是单位1，已知△ABC和△A1B1C1关于点O成中心对称，点O直线x上.
（1）在图中标出对称中心O的位置；
（2）画出△A1B1C1关于直线x对称的△A2B2C2；
（3）△ABC与△A2B2C2满足什么几何变换?