一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲
地的距离为y1千米，出租车离甲地的距离为y2千米，两车行驶的时间为x小时，y1、y2关于x的函数图像如下图
所示：
（1）根据图像，直接写出y1、y2关于x的函数关系式；
（2）若两车之间的距离为S千米，请写出S关于x的函数关系式；
（3）甲、乙两地间有A、B两个加油站，相距200千米，若客车进入A加油站时，出租车恰好进入B加油站，求A加油站离甲地的距离.
已知
求
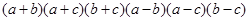的值。
如图，点P在∠AOB内，M、N分别是点P关于AO、BO的对称点，MN分别交AO，BO于点E、F，若△PEF的周长等于20㎝，求MN的长。
如图，AE=CF，AD∥BC，AD=CB。求证：△ADF≌△CBE
用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。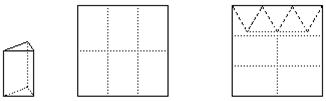
A方法 B方法
现有38张硬纸板，裁剪时x张用A方法，其余用B方法。
(1)、用x的代数式分别表示裁剪出的侧面和底面的个数；
(2)、若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
已知：AB∥CD，∠B +∠D＝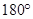
，判断直线BC与ED的位置关系并请说明理由.