如图,△ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F。
(1)试说明△ABD≌△BCE;
(2)△AEF与△ABE相似吗?说说你的理由;
(3)BD2=AD·DF成立吗?若成立,请说明理由。
在一次强风中,一块平地上一棵大树从离地面 处6米处折断倒下,量得树梢
处6米处折断倒下,量得树梢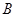 处与树底
处与树底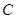 处的长是8米,树干
处的长是8米,树干 与地面
与地面 垂直.试通过计算求出这棵大树原来的高度.
垂直.试通过计算求出这棵大树原来的高度.
先化简,再求值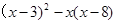 ,其中
,其中 ,且
,且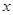 为整数.
为整数.
如图,正方形网格中的每个小正方形的边长都是,每个小格的顶点叫做格点.在正方形网格图①和图②中分别画一个三角形.
要求:(1)这个三角形的一个顶点为格点A,其余顶点从格点B、C、D、E、F、G、H中选取;
(2)这个三角形的各边均为无理数且不是等腰三角形.
给出三个整式a2,b2和2ab.
(1)当a=3,b=4时,求a2+b2+2ab的值.
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解.请写出你所选的式子及因式分解的过程.
利用简便方法计算: