如图，在平面直角坐标系中，点0为坐标原点，直线
交x轴于点A，交y轴于点B，BD平分∠AB0，点C是x轴的正半轴上一点，连接BC，且AC=AB．
（1）求直线BD的解析式：
（2）过C作CH∥y轴交直线AB于点H，点P是射线CH上的一个动点，过点P作PE⊥CH，直线PE交直线BD于E、交直线BC于F，设线段EF的长为d(d≠0)，点P的纵坐标为t，求d与t之间的函数关系式，并写出自变量t的取值范围；
（3）在（2）的条件下，取线段AB的中点M，y轴上有一点N．试问：是否存在这样的t的值，使四边形PEMN是平行四边形，若存在，请求出t的值；若不存在，请说明理由．
观察下列等式，探究其中的规律：
（1）根据以上观察，计算：① 
② 
（2）猜想：当n为自然数时，
如图，长方形的长为
，宽为
，
（1）用含、的代数式表示右图阴影部分的面积S阴影．
（2）当a=5
，b=2时，求S阴影．（
取3．14）
张亮用470元钱购买了8套儿童服装，准备以一定的价格出售．如果每套儿童服装以70元的价格作为标准价格来卖，超出为＋，不足为－，那么8套儿童服装的销售记录如下（单位：元）：
7 ， －3 ，－1 ，－8 ，－2 ，＋9 ， 0 ，＋6
当他卖完这8套服装盈利还是亏损，盈利或亏损多少元？
已知：
与
互为相反数，
与
互为倒数，当
时，求代数式
的值．
在所给的数轴上表示下列四个数，并把这四个数按从小到大的顺序，用“＜”号连接起来．
－3， 0，－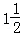
， 1
用“＜”号连接起来： ＜ ＜ ＜