如图，在平面直角坐标系中，O为坐标原点，点A、B的坐标分别为（8，0）、（0，6）．动点Q从点O、动点P从点A同时出发，分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动，运动时间为t（秒）（0＜t≤5）．以P为圆心，PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D，连结CD、QC．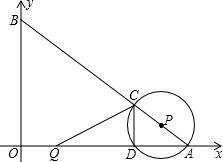
（1）求当t为何值时，点Q与点D重合？
（2）设△QCD的面积为S，试求S与t之间的函数关系，并求S的最大值？
（3）若⊙P与线段QC只有一个交点，请直接写出t的取值范围．
如图，在平面直角坐标系中，△ABC和△
是以坐标原点O为位似中心的位似图形，且点B（3，1），B′（6，2）.
（1）请你根据位似的特征并结合点B的坐标变化回答下列问题： ①若点A（
，3），则A′的坐标为；②△ABC与△的相似比为；
（2）若△ABC的面积为m，求△A′B′C′的面积.（用含m的代数式表示）
将分别标有数字1、2、3的三张卡片洗匀后，背面朝上放在桌面上．
（1）若随机地抽取一张，则抽到数字恰好为1的概率是；
（2）请你通过列表或画树状图分析：先随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，求组成的两位数能被4整除的概率.
在数学活动课中，小张为了测量校园内旗杆AB的高度，站在教学楼的顶端C处测得旗杆底端B的俯角为45°，测得旗杆顶端A的仰角为30°，已知旗杆与教学楼的水平距离CD为10m.
（1）直接写出教学楼CE的高度；
（2）求旗杆AB的高度.（结果保留根号）
先化简,再求值：
，其中
．
解方程: （1）
（2）