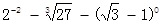端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转装盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.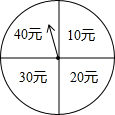
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
(1)写出y与t之间的函数关系式.
(2)通话2分钟应付通话费多少元?
(3)通话7分钟呢?
已知:y + 2与3x成正比例,且当x = 1时,y的值为4 .
(1)求y与x之间的函数关系式;
(2)若点(m−1,a)、点(m+2,b)(m为常数)是该函数图像上的两点,试比较a、b的大小,并说明理由.
如图示,△ABC中点D在边AC上,DB=BC,E是CD的中点,F是AB的中点.
求证:EF=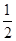 AB.
AB.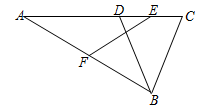
点A(-1,4)和点B(-5,1)在平面直角坐标系中的位置如图所示.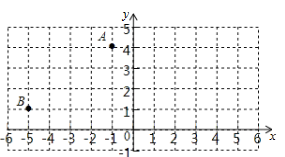
(1)将点A、B分别向右平移5个单位,得到点A1、B1,请画出四边形AA1B1B;
(2)画一条直线,将四边形AA1B1B分成两个全等的图形,并且每个图形都是轴对称图形.
(1)求x的值:4(x+1)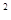 =64
=64
(2)计算: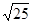 +
+