如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．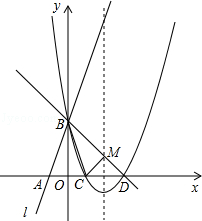
（1）求直线BD和抛物线的解析式．
（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．
（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．
列方程解应用题：
某一工程进行招标时，接到了甲、乙两个工程队的投标书，施工1天需付甲工程队工程款1.5万元，付乙工程队工程款1.1万元，工程领导小组根据甲、乙两队的投标书测算，可有三种施工方案：
方案（1）：甲工程队单独完成这项工程，刚好如期完成；
方案（2）：乙工程队单独完成这项工程，要比规定日期多5天；
方案（3）：若甲、乙两队合作4天，余下的工程由乙工程队单独做，也正好如期完成；
在不耽误工期的情况下，你觉得哪种方案最省钱？请说明理由。
已知：
与
成正比例，且
时，
。
（1）试求
与之间的函数关系式；
（2）当
时，求的值；
（3）当取何值时，
？；
已知：如图，四边形ABCD，AB=8，BC=6，CD=26，AD=24，且AB⊥BC。
求：四边形ABCD的面积。
解方程：
（1）
（2）
先化简代数式
，然后选取一个使原式有意义的
的值代入求值.