已知椭圆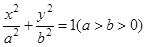 的离心率为
的离心率为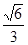 ,且过点
,且过点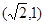 .
.
(1)求椭圆的方程;
(2)若过点C(-1,0)且斜率为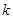 的直线
的直线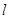 与椭圆相交于不同的两点
与椭圆相交于不同的两点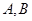 ,试问在
,试问在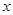 轴上是否存在点
轴上是否存在点 ,使
,使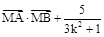 是与
是与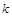 无关的常数?若存在,求出点
无关的常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知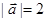 ,
,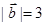 ,
, 与
与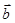 的夹角为
的夹角为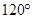 。求:
。求:
(1)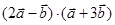 ;
;
(2)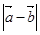 ;
;
(3)若在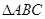 中,
中, ,求
,求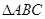 的面积。
的面积。
已知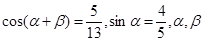 均为锐角,求
均为锐角,求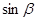 的值。
的值。
(本小题满分13分)
如图, 为平面的一组基向量,
为平面的一组基向量, ,
, ,
, 与
与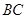 交与点
交与点
(1)求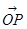 关于
关于 的分解式;(2)设
的分解式;(2)设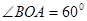 ,
,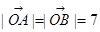 ,求
,求 ;
;
(3)过 任作直线
任作直线 交直线
交直线 于
于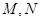 两点,设
两点,设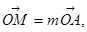
 ,
,
( )求
)求 的关系式。
的关系式。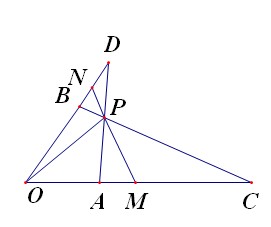
(本小题满分13分)
已知对任意平面向量 ,把
,把 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角得到向量
角得到向量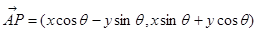 ,叫做把点
,叫做把点 绕点
绕点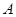 逆时针方向旋转角得到点
逆时针方向旋转角得到点 。
。
(1)已知平面内点 ,点
,点 。把点
。把点 绕点
绕点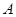 沿逆时针旋转
沿逆时针旋转 后得到点
后得到点 ,求点
,求点 的坐标;
的坐标;
(2)设平面内直线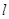 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转 后得到的点组成的直线方程是
后得到的点组成的直线方程是 ,求原来的直线
,求原来的直线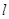 方程。
方程。
(本小题满分13分)
△ABC的面积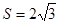 ,且
,且
(1) 求角 的大小;(2)若
的大小;(2)若 且
且 求
求