如图,已知曲线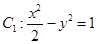 ,曲线
,曲线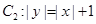 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与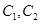 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.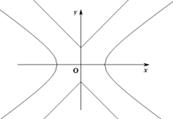
(1)在正确证明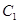 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线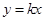 与
与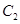 有公共点,求证
有公共点,求证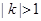 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆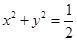 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
已知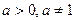 ,数列
,数列 的前
的前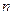 项和
项和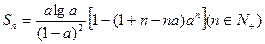 ,若数列
,若数列 的每一项总小于它后面的项,求
的每一项总小于它后面的项,求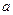 的取值范围.
的取值范围.
⑴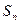 为等差数列
为等差数列 的前
的前 项和,
项和, ,
,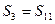 ,问数列的前几项和最大?
,问数列的前几项和最大?
⑵公差不为零的等差数列 中,
中, ,
,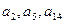 成等比数列,求数列
成等比数列,求数列 的前
的前 项和
项和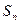 .
.
由原点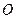 向三次曲线
向三次曲线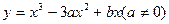 引切线,切于不同于点
引切线,切于不同于点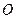 的点
的点 ,再由
,再由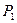 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于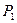 的点
的点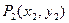 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列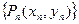 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求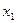 ; (2)求
; (2)求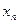 与
与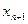 的关系式;
的关系式;
(3)若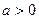 ,求证:当
,求证:当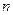 为正偶数时,
为正偶数时,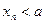 ;当
;当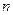 为正奇数时,
为正奇数时,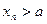 .
.
夏季高山上的温度从脚起,每升高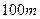 ,降低
,降低 ℃,已知山顶处的温度是
℃,已知山顶处的温度是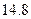 ℃,山脚处的温度为
℃,山脚处的温度为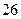 ℃,问此山相对于山脚处的高度是多少米.
℃,问此山相对于山脚处的高度是多少米.
数列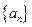 首项
首项 ,前
,前 项和
项和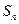 与
与 之间满足
之间满足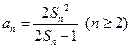
(1)求证:数列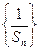 是等差数列(2)求数列
是等差数列(2)求数列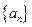 的通项公式
的通项公式
(3)设存在正数 ,使
,使 对于一切
对于一切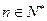 都成立,求
都成立,求 的最大值。
的最大值。