如图甲所示,两平行金属板的板长不超过0.2 m,板间的电压u随时间t变化的图线如图乙所示,在金属板右侧有一左边界为MN、右边无界的匀强磁场,磁感应强度 ,方向垂直纸面向里.现有带正电的粒子连续不断地以速度
,方向垂直纸面向里.现有带正电的粒子连续不断地以速度 ,沿两板间的中线
,沿两板间的中线 平行金属板射入电场中,磁场边界MN与中线
平行金属板射入电场中,磁场边界MN与中线 垂直.已知带电粒子的比荷
垂直.已知带电粒子的比荷 ,粒子所受的重力和粒子间的相互作用力均忽略不计.
,粒子所受的重力和粒子间的相互作用力均忽略不计.
(1)在每个粒子通过电场区域的时间内,可以把板间的电场强度看作是恒定的.试说明这种处理能够成立的理由.
(2)设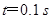 时刻射入电场的带电粒子恰能从平行金属板边缘射出,求该带电粒子射出电场时的速度大小.
时刻射入电场的带电粒子恰能从平行金属板边缘射出,求该带电粒子射出电场时的速度大小.
(3)对于所有经过电场射入磁场的带电粒子,设其射入磁场的入射点和从磁场射出的出射点间的距离为d,试判断d的大小是否随时间而变化?若不变,证明你的结论;若变,求出d的变化范围.

如图所示,物体A质量4kg,物体B质量2kg,A与B、A与地的动摩擦因数相同,物体B用细绳系住,当水平力F= 32N时,才能将A匀速拉出,求接触面间的动摩擦因数?(g=10m/s2)
汽车在高速公路上行驶,若驾驶员发现前方75m处发生了交通事故而堵住了车道,驾驶员经过0.5s反应后才开始刹车,并以恒定的加速度做匀减速直线运动,加速度大小为7.5m/s2,,则恰好在事故车面前停下,已知高速公路上限速110km/h,试分析该汽车是否超速?
一列火车进站前先关闭汽阀,让车做匀减速滑行,此时速度为20m/s,当火车滑行300 m时,速度为10m/s;此后又继续滑而停止在车站中,设火车在滑行过程中加速度始终保持不变。试求:
(1)火车滑行的加速度;
(2)火车从关闭汽阀到停止滑行时,滑行的总时间。
一电路如图所示,电源电动势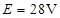 ,内阻
,内阻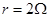 ,电阻
,电阻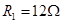 ,
,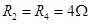 ,
,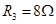 ,C为平行板电容器,其电容C=3.0pF,虚线到两极板距离相等,极板长
,C为平行板电容器,其电容C=3.0pF,虚线到两极板距离相等,极板长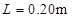 ,两极板的间距
,两极板的间距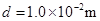 。
。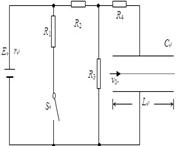
(1)若开关S处于断开状态,则当其闭合后,求流过R4的总电量为多少?
(2)若开关S断开时,有一带电微粒沿虚线方向以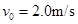 的初速度射入C的电场中,刚好沿虚线匀速运动,问:当开关S闭合后,此带电微粒以相同初速度沿虚线方向射入C的电场中,能否从C的电场中射出?(要求写出计算和分析过程,g取
的初速度射入C的电场中,刚好沿虚线匀速运动,问:当开关S闭合后,此带电微粒以相同初速度沿虚线方向射入C的电场中,能否从C的电场中射出?(要求写出计算和分析过程,g取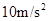 )
)
如图所示是利用电动机提升重物的示意图,其中D是直流电动机.p是一个质量为m的重物,它用细绳拴在电动机的轴上.闭合开关s,重物p以速度v被匀速提升,这时电流表和电压表的示数分别是I=5.0A和U=110V,重物p上升的速度v=0.90m/s.重物的质量m=50kg。不计一切摩擦,g取10m/s2.求: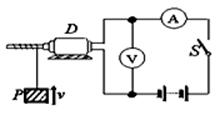
(1)电动机消耗的电功率P电;
(2)电动机线圈的电阻R。