(本小题满分12分)
一个不透明的袋子中装有4个形状相同的小球,分别标有不同的数字2,3,4,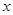 ,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表
| 摸球总次数 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
| “和为7”出现的频数 |
1 |
9 |
14 |
24 |
26 |
37 |
58 |
82 |
109 |
150 |
| “和为7”出现的频率 |
0.10 |
0.45 |
0.47 |
0.40 |
0.29 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
(参考数据: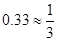 )
)
(Ⅰ)如果试验继续下去,根据上表数据,出现“数字之和为7”的频率将稳定在它的概率附近。试估计“出现数字之和为7”的概率,并求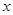 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,设定一种游戏规则:每次摸2球,若数字和为7,则可获得奖金7元,否则需交5元。某人摸球3次,设其获利金额为随机变量 元,求
元,求 的数学期望和方差。
的数学期望和方差。
已知函数
.
(Ⅰ) 求
的值;
(Ⅱ) 若
,求
.
设F为抛物线E: 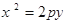
 的焦点,A、B、C为该抛物线上三点,已知
的焦点,A、B、C为该抛物线上三点,已知 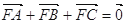 且
且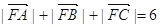 .
.
(1)求抛物线方程;
(2)设动直线l与抛物线E相切于点P,与直线 相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过 小时收费
小时收费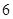 元,超过
元,超过 小时的部分每小时收费
小时的部分每小时收费 元(不足
元(不足 小时的部分按
小时的部分按 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过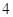 小时.
小时.
(1)若甲停车 小时以上且不超过
小时以上且不超过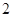 小时的概率为
小时的概率为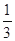 ,停车付费多于
,停车付费多于 元的概率为
元的概率为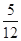 ,求甲停车付费恰为
,求甲停车付费恰为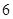 元的概率;
元的概率;
(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为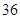 元的概率.
元的概率.
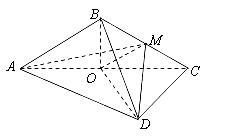
如图,菱形 的边长为6,
的边长为6,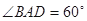 ,
,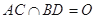 .将菱形
.将菱形 沿对角线
沿对角线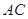 折起,得到三棱锥 ,点
折起,得到三棱锥 ,点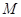 是棱
是棱 的中点,
的中点, .
.
(1)求证: ;
;
(2)求三棱锥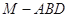 的体积.
的体积.
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有 位学生,每次活动均需该系 位学生参加( 和 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为 .
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使
取得最大值的整数
.