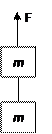(9分)一辆汽车的质量是5×10 kg,发动机的额定功率为60kW,汽车所受阻力恒为2000N,如果汽车从静止开始以2m/s
kg,发动机的额定功率为60kW,汽车所受阻力恒为2000N,如果汽车从静止开始以2m/s 的加速度做匀加速直线运动,功率达到最大后汽车又以额定功率运动了一段距离达到了最大速度,在整个过程中汽车运动了100m。下面是甲、乙两位同学关于此过程中汽车牵引力做功的解法:
的加速度做匀加速直线运动,功率达到最大后汽车又以额定功率运动了一段距离达到了最大速度,在整个过程中汽车运动了100m。下面是甲、乙两位同学关于此过程中汽车牵引力做功的解法:
甲同学的解法: ①
①
W=Pt=6×10 ×10J=6×10
×10J=6×10 J ②
J ②
乙同学的解法:F=ma+f=5×10 ×2+2000=1.2×10
×2+2000=1.2×10 N ③
N ③
W=Fs=1.2×10 ×100J=1.2×10
×100J=1.2×10 J ④
J ④
请对上述两位同学的解法做出评价并说明理由。若你认为两同学的解法都不正确,请给出你的解法。
如图所示,倾角 =37°的斜面固定在水平面上。质量m=1.0kg的小物块受到沿斜面向上的F=9.0N的拉力作用,小物块由静止沿斜面向上运动。小物块与斜面间的动摩擦因数
=37°的斜面固定在水平面上。质量m=1.0kg的小物块受到沿斜面向上的F=9.0N的拉力作用,小物块由静止沿斜面向上运动。小物块与斜面间的动摩擦因数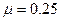 (斜面足够长,取g=l0m/s2。sin37°=0.6,cos37°=0.8)
(斜面足够长,取g=l0m/s2。sin37°=0.6,cos37°=0.8)
(1)求小物块运动过程中所受摩擦力的大小;
(2)求在拉力的作用过程中 ,小物块加速度的大小;
,小物块加速度的大小;
(3)若在小物块沿斜面向上运动0.80m时,将拉力F撤去,求此后小物块沿斜面向上运动的距离。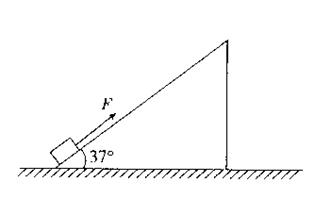
.如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒钟通过速度传感器测量物体的瞬时速度,下表给出了部分测量数据.(重力加速度g=10m/s2)
求:(1)斜面的倾角a;
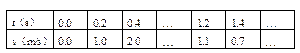 |
(2)物体与水平面之间的动摩擦因数m;
(3)t=0.6s时的瞬时速度v.
图所示,一水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0kg的小滑块.当圆盘转动的角速度达到某一数值时,滑块从圆盘边缘滑落,经光滑的过渡圆管进入轨道ABC.以知AB段斜面倾角为53°,BC段斜面倾角为37°,滑块与圆盘及斜面间的动摩擦因数均μ="0.5" ,A点离B点所在水平面的高度h=1.2m.滑块在运动过程中始终未脱离轨道,不计在过渡圆管处和B点的机械能损失,最大静摩擦力近似等于滑动摩擦力,取g=10m/s2,sin37°="0.6;" cos37°=0.8
(1)若圆盘半径R=0.2m,当圆盘的角速度多大时,滑块从圆盘上滑落?
(2)若取圆盘所在平面为零势能面,求滑块到达B点时的机械能.
(3)从滑块到达B点时起,经0.6s 正好通过C点,求BC之间的距离.
长L的轻杆两端分别固定有质量为m的小铁球,杆的三等分点O处有光滑的水平转动轴。用手将该装置固定在杆恰好水平的位置,然后由静止释放,当杆到达竖直位置时,求轴对杆的作用力F的大小和方向。
如图所示,质量分别为m1、m2的两个物块,中间用细绳相连,在F拉力的作用下一起向上做匀加速运动,求中间细绳的拉力为多大?