分某运动员做跳伞训练,他从悬停在空中的直升飞机上由静止跳下,跳离飞机一段时间后打开降落伞做减速下落。他打开降落伞后的速度时间图象如图a(t=0为打开伞瞬间)。降落伞用8根对称的绳悬挂运动员,每根绳与中轴线的夹角均为37°,如图b。已知人的质量为50kg,降落伞质量也为50kg,不计人所受的空气阻力,打开伞后降落伞所受阻力f与速度v成正比,即f=kv(g取10m/s2,sin53°=0.8,cos53°=0.6).求: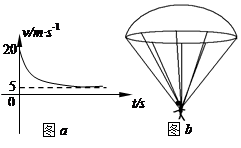
⑴打开降落伞前人自由下落的距离;
⑵阻力系数k;
⑶打开伞瞬间加速度a的大小和方向以及此时每根悬绳承受的拉力为多少。
在h高处,以初速度v0向水平方向抛出一个小球,不计空气阻力,小球着地时速度大小为多少?
将质量m=2kg的一块石头从离地面H=2m高处由静止开始释放,落入泥潭并陷入泥中h=5cm深处,不计空气阻力,求泥对石头的平均阻力。(g取10m/s2)
一架喷气式飞机,质量m=5×103kg,起飞过程中从静止开始滑跑的路程为s =5.3×102m时,达到起飞的速度v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02),求飞机受到的牵引力。
一个质量为2kg的小球从45m的高处自由下落,求2秒内的平均功率是多少?2秒末的瞬时功率是多少?
以质量为3kg的物块在水平面上以V=4m/s的速度运动,物块所具有的动能是多少?