如图所示，两个侧壁绝热、顶部和底部都导热的相同气缸直立放置，气缸底部和顶部均有细管连通，顶部的细管带有阀门K.两气缸的容积均为V0，气缸中各有一个绝热活塞(质量不同，厚度可忽略).开始时K关闭，两活塞下方和右活塞上方充有气体(可视为理想气体)，压强分别为
和
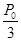;左活塞在气缸正中间，其上方为真空; 右活塞上方气体体积为
.现使气缸底与一恒温热源接触，平衡后左活塞升至气缸顶部，且与顶部刚好没有接触；然后打开K，经过一段时间，重新达到平衡.已知外界温度为
，不计活塞与气缸壁间的摩擦.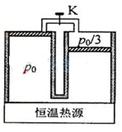
求:(1)恒温热源的温度T;
(2)重新达到平衡后左气缸中活塞上方气体的体积
.
在平直公路上以6m/s的速度匀速行驶的自行车与同向行驶的汽车同时经过A点,此时汽车速度为10m/s,并开始以0.5m/s2的加速度做减速行驶,而自行车仍然匀速前进.求：
(1)经过多长时间自行车追上汽车？
(2)自行车追上汽车时,汽车的速度多大？
以初速度为10m/s行驶的列车开始下坡加速运动，在坡路上的加速度大小为0.2m/s2，经过30s后到达坡底，求：
（1）列车到达坡底时的速度；（2）坡路的长度
如图所示，间距为L的光滑水平金属导轨，水平地放置在竖直方向的磁感应强度为B的匀强磁场中，一端接阻值为R的电阻．质量为m的导体棒放置在导轨上，其电阻为R0。在拉力F作用下从t＝0的时刻开始运动，其速度随时间的变化规律为v＝vmsinωt，不计导轨电阻．求：
(1)从t＝0到t＝时间内电阻R产生的热量．
(2)从t＝0到t＝时间内拉力F所做的功．
下图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置，设摆球向右方向运动为正方向，下图乙是这个单摆的振动图象，根据图象回答：
(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为9.86 m/s2， 试求这个摆的摆长是多少？
一居民小区有440户，以前每户平均消耗电功率为100W，使用的区间变压器匝数比为165：6，恰好能使额定电压为220V的用电器正常工作，现在因家用电器增加，每户平均消耗的电功率为250W，若变压器输入电压仍为6600V，区间输电线线路不变，为了使家用电器正常工作，需换用区间变压器，则此变压器的匝数比为多少？