如图所示,一辆质量M=3kg的小车A静止在光滑的水平面上,小车上有一质量m=1kg的光滑小球B,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为EP=6J,小球与小车右壁距离为L,解除锁定,小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住,求:(i)小球脱离弹簧时小球和小车各自的速度大小;
(ii)在整个过程中,小车移动的距离。
如图所示,电动机带着绷紧的传送带始终以v0=2 m/s的速度运动,传送带与水平面的夹角θ=30°,现把一质量为m=10kg的工件轻轻地放在皮带的底端,经过一段时间后,工件送到高h=2m的平台上,已知工件与皮带之间的动摩擦因数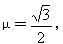 除此之外,不记其他损耗。求电动机由于传送工件多消耗的电能。(取g=10 m/s2)
除此之外,不记其他损耗。求电动机由于传送工件多消耗的电能。(取g=10 m/s2)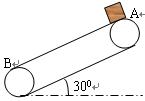
已知O、A、B、C为同一直线上的四点,AB间的距离为l1,BC间的距离为l2,一物体自O点静止起出发,沿此直线做匀加速运动,依次经过A、B、C三点。已知物体通过AB段与通过BC段所用时间相等。求O与A的距离。
F1是英文Formula One的缩写,即一级方程式赛车,是仅次于奥运会和世界杯的世界第三大赛事。F1 赛车的变速系统非常强劲,从时速0加速到100 km/h仅需2.3秒,此时加速度仍达10m/s2,时速为200 km/h时的加速度仍有3m/s2,从0加速到200 km/h再急停到0只需12秒。假定F1 赛车加速时的加速度随时间的增大而均匀减小,急停时的加速度大小恒为9.2 m/s2。上海F1赛道全长5.451km,比赛要求选手跑完56圈决出胜负。
求:
(1)若某车手平均时速为210km/h,则跑完全程用多长时间?
(2)该车手的F1 赛车的最大加速度。
据统计,城市交通事故大多因违章引起,在如图所示中,甲、乙两辆汽车分别在相互垂直的道路上,沿各自道宽的中心线(图中虚线所示)向前匀速行驶,当甲、乙两车的车头到十字路口(道路中心线)的距离分别为30m、40m时,道口恰处于红、绿灯转换甲、乙两车均未采取任何减速或制动等措施,以致两车相撞。已知两车型号相同,汽车的车长为5.2m,车宽为1.76m。并已知甲车的车速为v1=40km/h,设两车相撞前均匀速行使。试判断在穿过路口过程中,乙车车速的范围。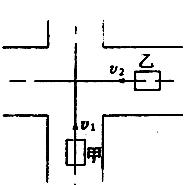
(9分)一辆值勤的警车停在公路边,当警员发现从他旁边以10 m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5 s后警车发动起来,并以2.5 m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90 km/h以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?(4分)
(2)警车发动后要多长时间才能追上货车?(5分)